题目内容
奇函数f(x)在{x|x≠0}上有定义,且在区间(0,+∞)上是增函数,f(2)=0,又函数g(t)=-t2+mt+3-2m,t∈[0,1],则使函数g(t),f(g(t))同取正值的m的范围
{m|m<0 }
{m|m<0 }
_.分析:由题意可得,当t∈[0,1]时,函数g(t)=-t2+mt+3-2m>0恒成立,故 g(0)=3-2m>0,且g(1)=2-m>0,由此解得 m的范围.要使f(g(t))>0,必须-2
<g(t)<0(舍去),或g(t)>2,即 t2-mt+2m-1<0在[0,1],恒成立.由
,解得 m的范围.再把这两个 m的范围取交集,即得所求.
<g(t)<0(舍去),或g(t)>2,即 t2-mt+2m-1<0在[0,1],恒成立.由
|
解答:解:由题意可得,当t∈[0,1]时,函数g(t)=-t2+mt+3-2m>0恒成立,
∴g(0)=3-2m>0,且g(1)=2-m>0,解得 m<
.
由奇函数f(x)在区间(0,+∞)上是增函数,f(2)=0,可得f(-2)=0,且f(x)在(-∞,0)上也是增函数.
要使f(g(t))>0,必须-2<g(t)<0(舍去),或g(t)>2. 即-t2+mt+3-2m>2在[0,1],恒成立,即 t2-mt+2m-1<0在[0,1],恒成立.
∴
,解得 m<0.
综上,使函数g(t),f(g(t))同取正值的m的范围是 {m|m<
}∪{m|m<0 }={m|m<0 },
故答案为 {m|m<0 }.
∴g(0)=3-2m>0,且g(1)=2-m>0,解得 m<
| 3 |
| 2 |
由奇函数f(x)在区间(0,+∞)上是增函数,f(2)=0,可得f(-2)=0,且f(x)在(-∞,0)上也是增函数.
要使f(g(t))>0,必须-2<g(t)<0(舍去),或g(t)>2. 即-t2+mt+3-2m>2在[0,1],恒成立,即 t2-mt+2m-1<0在[0,1],恒成立.
∴
|
综上,使函数g(t),f(g(t))同取正值的m的范围是 {m|m<
| 3 |
| 2 |
故答案为 {m|m<0 }.
点评:本题主要考查二次函数的性质,求二次函数在闭区间上的最值,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目
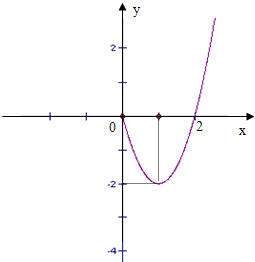 已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分,
已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分, 已知定义在R上奇函数f(x)在x≥0时的图象如图所示,
已知定义在R上奇函数f(x)在x≥0时的图象如图所示,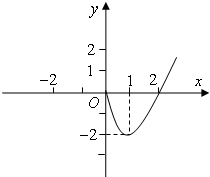 已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.
已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.