题目内容
已知定义在R上奇函数f（x）在x≥0时的图象如图所示，（1）补充完整f（x）在x≤0的函数图象；
（2）写出f（x）的单调区间；
（3）根据图象写出不等式xf（x）＜0的解集．
分析：（1）因为f（x）是奇函数得函数图象关于原点对称，可画出y轴左侧的图象，由此补出完整函数f（x）的图象即可；（2）可从图形直接观察得到写出f（x）的单调区间；
（3）利用两因式异号相乘得负，得出f（x）的正负，由图象可求出x的范围得结果．
（3）利用两因式异号相乘得负，得出f（x）的正负，由图象可求出x的范围得结果．
解答：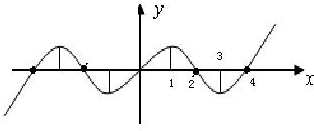
解：（1）因为函数为奇函数，故图一定关于原点对称，补出完整函数图象如图；
（2）单调增区间：[-1，1]，[3，+∞），（-∞，-3]；单调减区间：[-3，-1]，[1，3]
（3）x＞0时，f（x）＜0，∴2＜x＜4，
x＜0时，f（x）＞0，∴-4＜x＜-2，
∴不等式解集为：（2，4）∪（-4，-2）
解：（1）因为函数为奇函数，故图一定关于原点对称，补出完整函数图象如图；（2）单调增区间：[-1，1]，[3，+∞），（-∞，-3]；单调减区间：[-3，-1]，[1，3]
（3）x＞0时，f（x）＜0，∴2＜x＜4，
x＜0时，f（x）＞0，∴-4＜x＜-2，
∴不等式解集为：（2，4）∪（-4，-2）
点评：本题考查分段函数求解析式、作图，同时考查函数的函数的值域以及图解不等式．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目