题目内容
 (2011•朝阳区三模)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
(2011•朝阳区三模)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=| 1 |
| 2 |
| 3 |
(Ⅰ)若点M是棱PC的中点,求证:PA∥平面BMQ;
(Ⅱ)求证:平面PQB⊥平面PAD;
(Ⅲ)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
分析:(Ⅰ)本小题是一个证明线面平行的题,一般借助线面平行的判定定理求解,如图连接AC,交BQ于N,连接MN,先证明MN∥PA,再由线面平行的判定理证明线面平行;
(II)本小题是一个证明面面垂直的题,可采用面面垂直的定义求二面角是直角,或者用面面垂直的判定理证明,由题设条件知,利用面面垂直的判定定理证明较易,观察图形与题设条件,法一:可通过证明BQ⊥平面PAD来证明面面垂直;法二:可通过证明AD⊥平面PBQ.证明平面PQB⊥平面PAD;
(III)本小题研究二面角为30°时,确定M的位置,再由M的位置确定出t的值,由(II)由面面垂直的性质定理易得出Q点出发的三个线段QP,QA,QB两两垂直,故可以考虑建立空间坐标系利用空间向量将二面角的大小表示出来,利用二面角为30°建立方程求出t的值
(II)本小题是一个证明面面垂直的题,可采用面面垂直的定义求二面角是直角,或者用面面垂直的判定理证明,由题设条件知,利用面面垂直的判定定理证明较易,观察图形与题设条件,法一:可通过证明BQ⊥平面PAD来证明面面垂直;法二:可通过证明AD⊥平面PBQ.证明平面PQB⊥平面PAD;
(III)本小题研究二面角为30°时,确定M的位置,再由M的位置确定出t的值,由(II)由面面垂直的性质定理易得出Q点出发的三个线段QP,QA,QB两两垂直,故可以考虑建立空间坐标系利用空间向量将二面角的大小表示出来,利用二面角为30°建立方程求出t的值
解答:证明:(Ⅰ)连接AC,交BQ于N,连接MN. …(1分)
∵BC∥AD且BC=
AD,即BC
AQ,
∴四边形BCQA为平行四边形,且N为AC中点,
又∵点M在是棱PC的中点,
∴MN∥PA.…(2分)
∵MN?平面MQB,PA?平面MQB,…(3分)
∴PA∥平面MBQ. …(4分)
(Ⅱ)∵AD∥BC,BC=
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ.…(6分)
∵∠ADC=90°∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD,…(7分)
∴BQ⊥平面PAD. …(8分)
∵BQ?平面PQB,
∴平面PQB⊥平面PAD. …(9分)
另证:AD∥BC,BC=
AD,Q为AD的中点
∴BC∥DQ 且BC=DQ,
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°∴∠AQB=90° 即QB⊥AD. …(6分)
∵PA=PD,∴PQ⊥AD. …(7分)
∵PQ∩BQ=Q,∴AD⊥平面PBQ. …(8分)
∵AD?平面PAD,
∴平面PQB⊥平面PAD. …(9分)
(Ⅲ)∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD.…(10分)
(不证明PQ⊥平面ABCD直接建系扣1分)
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为
=(0,0,1);Q(0,0,0),P(0,0,
),B(0,
,0),C(-1,
,0).…(11分)
设M(x,y,z),
则
=(x,y,z-
),
=(-1-x,
-y,-z),
∵
=t
,
∴
,
∴
…(12分)
在平面MBQ中,
=(0,
,0),
=(-
,
,
),
∴平面MBQ法向量为
=(
,0,t).
∵二面角M-BQ-C为30°,cos30°=
=
=
,
∴t=3. …(13分)
∵BC∥AD且BC=
| 1 |
| 2 |
| ||
. |
∴四边形BCQA为平行四边形,且N为AC中点,
又∵点M在是棱PC的中点,
∴MN∥PA.…(2分)
∵MN?平面MQB,PA?平面MQB,…(3分)
∴PA∥平面MBQ. …(4分)
(Ⅱ)∵AD∥BC,BC=
| 1 |
| 2 |
∴四边形BCDQ为平行四边形,∴CD∥BQ.…(6分)
∵∠ADC=90°∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD,…(7分)
∴BQ⊥平面PAD. …(8分)
∵BQ?平面PQB,
∴平面PQB⊥平面PAD. …(9分)
另证:AD∥BC,BC=
| 1 |
| 2 |
∴BC∥DQ 且BC=DQ,
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°∴∠AQB=90° 即QB⊥AD. …(6分)
∵PA=PD,∴PQ⊥AD. …(7分)
∵PQ∩BQ=Q,∴AD⊥平面PBQ. …(8分)
∵AD?平面PAD,
∴平面PQB⊥平面PAD. …(9分)
(Ⅲ)∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD.…(10分)
(不证明PQ⊥平面ABCD直接建系扣1分)
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为
| n |
| 3 |
| 3 |
| 3 |
设M(x,y,z),
则
| PM |
| 3 |
| MC |
| 3 |
∵
| PM |
| MC |
∴
|
∴
|
在平面MBQ中,
| QB |
| 3 |
| QM |
| t |
| 1+t |
| ||
| 1+t |
| ||
| 1+t |
∴平面MBQ法向量为
| m |
| 3 |
∵二面角M-BQ-C为30°,cos30°=
| ||||
|
|
| t | ||
|
| ||
| 2 |
∴t=3. …(13分)
点评:本题考查与二面角有关的立体几何证明题,考查了二面角的求法,面面垂直的证明方法以及线面平行的证明,解题的关键是熟练掌握二面角的平面角的做法以及用向量法求二面角的步骤,面面垂直与线面平行的相关定理定义等,向量中的方程与立体几何中位置关系的对应,如数量积为0与垂直的对应,向量的共线与平行的对应,向量夹角与线线角,线面角,面面角的对应,本题考查了数形结合的思想,转化的思想,方程的思想,考查了待定系数建立方程的技巧,用向量解决立体几何问题的方法,本题知识性综合性强,考查空间想像能力,推理判断能力及转化的能力,本题运算量大,且多是符号运算,解题时要严谨

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
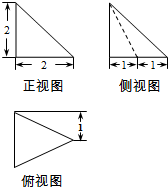 (2011•朝阳区三模)一空间几何体的三视图如图所示,则该几何体的体积为( )
(2011•朝阳区三模)一空间几何体的三视图如图所示,则该几何体的体积为( ) (2011•朝阳区三模)右图是一个几何体的三视图(单位:cm),根据图中数据,可得该几何体的体积是
(2011•朝阳区三模)右图是一个几何体的三视图(单位:cm),根据图中数据,可得该几何体的体积是