题目内容
(2011•朝阳区三模)已知椭圆
+y2=1的焦点分别为F1,F2,P为椭圆上一点,且∠F1PF2=90°,则点P的纵坐标可以是( )
| x2 |
| 4 |
分析:先根据椭圆的标准方程确定椭圆的几何量,再利用P为椭圆上一点,且∠F1PF2=90°,建立方程组,从而可求三角形的面积,进而利用等面积可求点P的纵坐标.
解答:解:设|PF1|=m,|PF2|=n,
椭圆
+y2=1中,a2=4,b2=1,c2=3,
∴a=2,b=1,c=
∵P为椭圆上一点,且∠F1PF2=90°,
∴
∴2mn=4
∴
mn=1
设点P的纵坐标为y,则
×2c×|y|=1
∴|y|=
故选B.
椭圆
| x2 |
| 4 |
∴a=2,b=1,c=
| 3 |
∵P为椭圆上一点,且∠F1PF2=90°,
∴
|
∴2mn=4
∴
| 1 |
| 2 |
设点P的纵坐标为y,则
| 1 |
| 2 |
∴|y|=
| ||
| 3 |
故选B.
点评:本题以椭圆的标准方程为载体,考查椭圆的性质,考查等面积的运用,属于基础题.

练习册系列答案
相关题目
 (2011•朝阳区三模)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
(2011•朝阳区三模)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=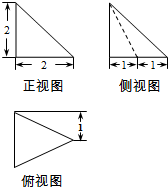 (2011•朝阳区三模)一空间几何体的三视图如图所示,则该几何体的体积为( )
(2011•朝阳区三模)一空间几何体的三视图如图所示,则该几何体的体积为( ) (2011•朝阳区三模)右图是一个几何体的三视图(单位:cm),根据图中数据,可得该几何体的体积是
(2011•朝阳区三模)右图是一个几何体的三视图(单位:cm),根据图中数据,可得该几何体的体积是