题目内容
(本小题满分12分)
如图,四棱锥 中,
中, 为矩形,平面
为矩形,平面 平面
平面 .
.
求证:

若 问
问 为何值时,四棱锥
为何值时,四棱锥 的体积最大?并求此时平面
的体积最大?并求此时平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
如图,四棱锥
 中,
中, 为矩形,平面
为矩形,平面 平面
平面 .
.求证:


若
 问
问 为何值时,四棱锥
为何值时,四棱锥 的体积最大?并求此时平面
的体积最大?并求此时平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.(1)详见解析,(2) 时,四棱锥的体积P-ABCD最大. 平面BPC与平面DPC夹角的余弦值为
时,四棱锥的体积P-ABCD最大. 平面BPC与平面DPC夹角的余弦值为
 时,四棱锥的体积P-ABCD最大. 平面BPC与平面DPC夹角的余弦值为
时,四棱锥的体积P-ABCD最大. 平面BPC与平面DPC夹角的余弦值为
试题分析:(1)先将面面垂直转化为线面垂直:ABCD为矩形,故AB
 AD,又平面PAD
AD,又平面PAD 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD=AD,所以AB
平面ABCD=AD,所以AB 平面PAD,再根据线面垂直证线线垂直:因为PD
平面PAD,再根据线面垂直证线线垂直:因为PD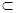 平面PAD,所以AB
平面PAD,所以AB PD
PD(2)求四棱锥体积,关键要作出高.这可利用面面垂直性质定理:过P作AD的垂线,垂足为O,又平面PAD
 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD=AD,所以PO
平面ABCD=AD,所以PO 平面ABCD,下面用
平面ABCD,下面用 表示高及底面积:设
表示高及底面积:设 ,则
,则 ,故四棱锥P-ABCD的体积为
,故四棱锥P-ABCD的体积为 故当
故当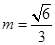 时,即
时,即 时,四棱锥的体积P-ABCD最大.
时,四棱锥的体积P-ABCD最大.求二面角的余弦值,可利用空间向量求解,根据题意可建立空间坐标系,分别求出平面BPC的法向量及
平面DPC的法向量,再利用向量数量积求夹角余弦值即可.
试题解析:(1)证明:ABCD为矩形,故AB
 AD,
AD,又平面PAD
 平面ABCD
平面ABCD平面PAD
 平面ABCD=AD
平面ABCD=AD所以AB
 平面PAD,因为PD
平面PAD,因为PD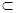 平面PAD,故AB
平面PAD,故AB PD
PD(2)解:过P作AD的垂线,垂足为O,过O作BC的垂线,垂足为G,连接PG.
故PO
 平面ABCD,BC
平面ABCD,BC 平面POG,BC
平面POG,BC PG
PG在直角三角形BPC中,
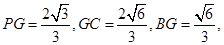
设
 ,则
,则 ,故四棱锥P-ABCD的体积为
,故四棱锥P-ABCD的体积为
因为
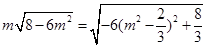
故当
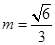 时,即
时,即 时,四棱锥的体积P-ABCD最大.
时,四棱锥的体积P-ABCD最大.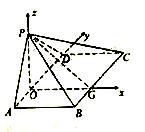
建立如图所示的空间直角坐标系,

故
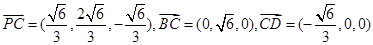
设平面BPC的法向量
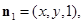 ,则由
,则由 ,
, 得
得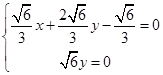
解得


同理可求出平面DPC的法向量
 ,从而平面BPC与平面DPC夹角
,从而平面BPC与平面DPC夹角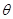 的余弦值为
的余弦值为

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 CD=1,PD=
CD=1,PD= .
.
 ?
? 中,
中, ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,
, 分别为线段
分别为线段 的中点.
的中点.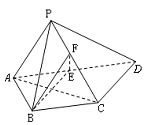
 ;
;  ⊥平面
⊥平面 .
.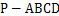 的底面
的底面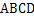 是平行四边形,
是平行四边形,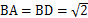 ,
,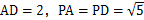 ,
,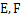 分别是棱
分别是棱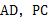 的中点.
的中点.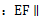 平面
平面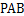 ;
;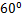 ,
,
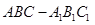 中,点
中,点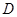 在边
在边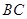 上,
上,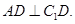
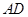
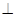 平面
平面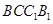 ;
; 是
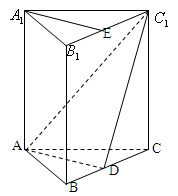
是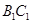 的中点,求证:
的中点,求证: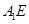 //平面
//平面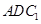 .
.

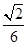 ,求线段AM的长.
,求线段AM的长.
 中,
中, ,
, 面
面 ,
, ,求面
,求面 与面
与面 所成二面角的正切值.
所成二面角的正切值.