题目内容
11.若函数f(x)是定义在(t,t2-3t-8)上的偶函数,则实数t的值是-2.分析 由函数的奇偶性定义可得t+t2-3t-8=0,解方程验证可得.
解答 解:由函数的奇偶性定义可得t+t2-3t-8=0,
整理并分解因式可得(t+2)(t-4)=0,
解得t=-2或t=4
当t=-2时,区间为(-2,2)符合题意,
当t=4时,区间为(4,-4),不符合题意,
故答案为:-2
点评 本题考查函数的奇偶性,涉及一元二次方程的解法,属基础题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.已知f(sinx)=cos3x,x∈[-90°,90°],则f(cos10°)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
6.若R上的奇函数y=f(x)满足f(x)=f(2-x),且当x∈(0,1]时,f(x)=log3x,则方程f(x)=-$\frac{1}{3}$+f(0)在区间(2016,2018)内的所有实限之和为( )
| A. | 4032 | B. | 4036 | C. | 4034 | D. | 4030 |
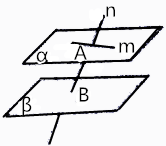 如图中,直线m,n,平面α、β,直线m与平面α之间的位置关系.
如图中,直线m,n,平面α、β,直线m与平面α之间的位置关系.