题目内容
(1)已知 ,
, ,求证:
,求证: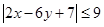 ;
;
(2)已知正数 满足关系
满足关系 ,求证:
,求证: .
.
 ,
, ,求证:
,求证: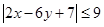 ;
;(2)已知正数
 满足关系
满足关系 ,求证:
,求证: .
.(1)根据两个数和差的绝对值大于等于绝对值的差,小于等于绝对值的和来得到证明。
(2)根据已知中两个正数和为定值,那么将所求的左侧运用配方法的思想来得到和与积的关系,借助于均值不等式得到证明。
(2)根据已知中两个正数和为定值,那么将所求的左侧运用配方法的思想来得到和与积的关系,借助于均值不等式得到证明。
试题分析:
解:(1)
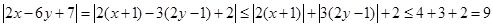 ;6分
;6分(2)因为正数
 满足关系
满足关系
 12分
12分点评:解决的关键是利用放缩法思想,以及均值不等式来构造定值求解最值的思想证明,属于基础题。

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
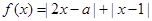 .
. 的解集;
的解集; 对
对 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.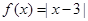 ,
,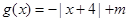
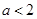 ,解关于
,解关于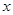 的不等式
的不等式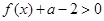 ;
; 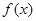 的图象恒在函数
的图象恒在函数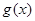 图象的上方,求实数
图象的上方,求实数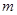 的取值范围.
的取值范围. 对任意实数x总成立,则a的取值范围是 ( )
对任意实数x总成立,则a的取值范围是 ( )



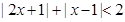 的解集为
的解集为 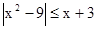
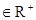 且
且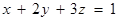 ,求
,求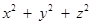 的最小值.
的最小值.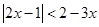 的解集为( )
的解集为( )


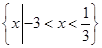
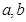 满足
满足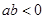 ,则下列不等式成立的是( )
,则下列不等式成立的是( )


