题目内容
关于函数f(x)=4sin(2x+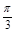 )(x∈R),有下列命题:
)(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是 的整数倍;
的整数倍;
②y= f(x)的表达式可改写为y=4cos(2x- );
);
③y= f(x)的图象关于点(- ,0)对称;
,0)对称;
④y= f(x)的图象关于直线x=- 对称.
对称.
其中正确的命题的序号是 .
②③
解析试题分析:∵f(x)=4sin(2x+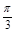 ),(x∈R)的周期为π,
),(x∈R)的周期为π,
当x1=- ,x2=
,x2=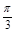
时,f(x1)=f(x2)=0,x1-x2 = ≠kπ,k∈z,故①是错误的.
≠kπ,k∈z,故①是错误的.
∵由诱导公式可得f(x)=4sin(2x+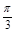 )=4cos(
)=4cos( -2x-
-2x-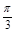 )=4cos(
)=4cos( -2x)=4cos(2x-
-2x)=4cos(2x- ),故 ②正确.
),故 ②正确.
∵当 x=- 时,f(x)=0,即点(-
时,f(x)=0,即点(- ,0)是f(x)与x轴的交点,是对称中心,故③正确.
,0)是f(x)与x轴的交点,是对称中心,故③正确.
∵当 x=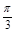 时,f(x)=4sin(2x+
时,f(x)=4sin(2x+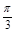 )=0,不是f(x)的最值,故④是错误的.
)=0,不是f(x)的最值,故④是错误的.
综上知,答案为②③。
考点:本题主要考查正弦型函数的对称性、单调性、周期性,诱导公式的应用。
点评:典型题,通过举反例说明命题不正确,通过推证说明命题正确,是解答此类问题的常用方法。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 的最大值是
的最大值是  是定义在
是定义在 上的周期为2的偶函数,当
上的周期为2的偶函数,当 时,
时,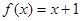 ,则
,则 =___________.
=___________. 是实数.若函数
是实数.若函数 是定义在
是定义在 上的奇函数,但不是偶函数,则函数
上的奇函数,但不是偶函数,则函数 的递增区间为__________;
的递增区间为__________;  的零点属于区间
的零点属于区间 ,则
,则 .
. 的单调增区间是 .
的单调增区间是 .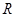 上的函数
上的函数 满足:
满足: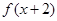 是偶函数,且
是偶函数,且 时的解析式为
时的解析式为 ,则
,则 时
时 的解析式为 ;
的解析式为 ;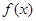 的定义域为A,若
的定义域为A,若 则称
则称 是单函数.下列命题:
是单函数.下列命题: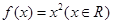 是单函数;
是单函数; ;
; 为单函数,则对于任意b
为单函数,则对于任意b B,它至多有一个原象;
B,它至多有一个原象;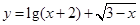 的定义域为 。
的定义域为 。