题目内容
设函数 是定义在
是定义在 上的周期为2的偶函数,当
上的周期为2的偶函数,当 时,
时,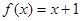 ,则
,则 =___________.
=___________.

解析试题分析::∵函数f(x)是定义在R上的周期为2的函数,
∴f( )=f(-
)=f(- +2)=f(-
+2)=f(- ),
),
又∵函数f(x)是定义在R上的偶函数,
∴f(- )=f(
)=f( ),
),
又∵当x∈[0,1]时,f(x)=x+1,
∴有:f( )=
)= +1=
+1= ,
,
则f( )=
)= .
.
故答案为 .
.
考点:函数的奇偶性、单调性、周期性。
点评:中档题,利用函数的周期性先把f( )转化成f(-
)转化成f(- ),再利用函数f(x)是定义在R上的偶函数转化成f(
),再利用函数f(x)是定义在R上的偶函数转化成f( ),代入已知求解即可。此题较为典型。
),代入已知求解即可。此题较为典型。

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 。
。 的定义域为
的定义域为 ,则函数
,则函数 的定义域为 __________________________
的定义域为 __________________________  (
( ),满足:
),满足: ,且
,且 时,
时, ,则函数
,则函数 图像的交点个数为 .
图像的交点个数为 . 是奇函数,如果
是奇函数,如果 ,那么
,那么 _______
_______ 的定义域为 .
的定义域为 .  ,对任意
,对任意 ,
, 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .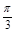 )(x∈R),有下列命题:
)(x∈R),有下列命题:  的整数倍;
的整数倍;  );
);  ,则
,则 .
.