题目内容
给出下列命题:
①已知函数y=2sinωx的图象与直线y=2的某两个交点的横坐标为x1,x2,若|x1-x2|的最小值为π,则ω=2;
②向量
与
满足|
•
|=|
|•|
|,则
与
共线;
③已知幂函数y=xm2-2m-3(m∈N)的图象与坐标轴不相交,且关于y轴对称,则m=1;
其中所有正确命题的序号是
①已知函数y=2sinωx的图象与直线y=2的某两个交点的横坐标为x1,x2,若|x1-x2|的最小值为π,则ω=2;
②向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
③已知幂函数y=xm2-2m-3(m∈N)的图象与坐标轴不相交,且关于y轴对称,则m=1;
其中所有正确命题的序号是
②
②
.分析:①依题意,可知y=2sinωx的周期T=π,从而可知ω=±2,可判断①的正误;
②利用向量的数量积可判断其正误;
③依题意,解不等式m2-2m-3<0且m2-2m-3为偶数即可判断③的正误.
②利用向量的数量积可判断其正误;
③依题意,解不等式m2-2m-3<0且m2-2m-3为偶数即可判断③的正误.
解答:解:①依题意,可知y=2sinωx的周期T=
=π,
∴ω=±2,故①错误;
②∵|
•
|=||
|•|
|cos<
,
>|=|
|•|
|,
∴|cos<
,
>|=1,
∴<
,
>=0或π,
∴
与
共线,故②正确;
③依题意,m2-2m-3≤0且m2-2m-3为偶数,
∴-1≤m≤3且m2-2m-3为偶数,
∴m=-1或m=1或m=3,故③错误;
综上所述,正确命题的序号是②.
故答案为:②.
| 2π |
| |ω| |
∴ω=±2,故①错误;
②∵|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴|cos<
| a |
| b |
∴<
| a |
| b |
∴
| a |
| b |
③依题意,m2-2m-3≤0且m2-2m-3为偶数,
∴-1≤m≤3且m2-2m-3为偶数,
∴m=-1或m=1或m=3,故③错误;
综上所述,正确命题的序号是②.
故答案为:②.
点评:本题考查命题的真假判断与应用,考查共线向量与平面向量数量积的运算,考查幂函数的性质与应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.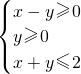 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.