题目内容
给出下列命题:①、已知函数y=f(x).(x∈R),则y=f(x-1)的图象与y=f(1-x)的图象关于直线x=1对称;
②、设函数f(x)=cos(x+φ),则“f(x)为偶函数”的充要条件是“f'(0)=0”;
③、等比数列{an}的前n项和为Sn,则“公比q>0”是“数列{Sn}单增”的充要条件;
④、实数x,y,则“
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.其中真命题有 (写出你认为正确的所有真命题的序号).
【答案】分析:在y=f(x-1)的图象上任取一点P(a,b),则有b=f(a-1)=f[1-(2-a)],故点P(a,b)关于直线x=1的对称点P'(2-a,b)在y=f(1-x)的图象上,所以y=f(x-1)与y=f(1-x)的图象关于直线x=1对称;f(x)为偶函数?f(0)=±1?cosφ=±1?sinφ=0?f'(0)=0;公比q>0不能得到{Sn}单增,如an=-2n.Sn=2-2n+1单减.{Sn}单增?an>0,(n≥2)成立⇒q>0;不等式“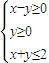 ”表示的平面区域为△ABC,不等式“|2y-x|≤2”表示的平面区域为两条平行直线l和m之间的部分,前者为后者的真子集.
”表示的平面区域为△ABC,不等式“|2y-x|≤2”表示的平面区域为两条平行直线l和m之间的部分,前者为后者的真子集.
解答:解析:①、正确.在y=f(x-1)的图象上任取一点P(a,b),则有b=f(a-1)=f[1-(2-a)],故点P(a,b)关于直线x=1的对称点P'(2-a,b)在y=f(1-x)的图象上,所以y=f(x-1)与y=f(1-x)的图象关于直线x=1对称;提示:若函数y=f(x)满足f(x-1)=f(1-x),则y=f(x)的图象关于直线x=0对称.
②、正确.f(x)为偶函数?f(0)=±1?cosφ=±1?sinφ=0?f'(0)=0
③、错误.充分性不成立.公比q>0不能得到{Sn}单增,如an=-2n.Sn=2-2n+1单减.
必要性成立.{Sn}单增?an>0,(n≥2)成立⇒q>0.
④、正确.如图,不等式“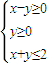 ”表示的平面区域为△ABC,不等式“|2y-x|≤2”表示的平面区域为两条平行直线l和m之间的部分,前者为后者的真子集,故命题正确.
”表示的平面区域为△ABC,不等式“|2y-x|≤2”表示的平面区域为两条平行直线l和m之间的部分,前者为后者的真子集,故命题正确.
故答案为:①②④.
点评:本题考查必要条件、充分条件和充要条件的判断,解题时要认真审题,注意函数的对称性、奇偶性、单调性和可行域的灵活运用.
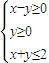 ”表示的平面区域为△ABC,不等式“|2y-x|≤2”表示的平面区域为两条平行直线l和m之间的部分,前者为后者的真子集.
”表示的平面区域为△ABC,不等式“|2y-x|≤2”表示的平面区域为两条平行直线l和m之间的部分,前者为后者的真子集.解答:解析:①、正确.在y=f(x-1)的图象上任取一点P(a,b),则有b=f(a-1)=f[1-(2-a)],故点P(a,b)关于直线x=1的对称点P'(2-a,b)在y=f(1-x)的图象上,所以y=f(x-1)与y=f(1-x)的图象关于直线x=1对称;提示:若函数y=f(x)满足f(x-1)=f(1-x),则y=f(x)的图象关于直线x=0对称.
②、正确.f(x)为偶函数?f(0)=±1?cosφ=±1?sinφ=0?f'(0)=0
③、错误.充分性不成立.公比q>0不能得到{Sn}单增,如an=-2n.Sn=2-2n+1单减.
必要性成立.{Sn}单增?an>0,(n≥2)成立⇒q>0.
④、正确.如图,不等式“
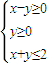 ”表示的平面区域为△ABC,不等式“|2y-x|≤2”表示的平面区域为两条平行直线l和m之间的部分,前者为后者的真子集,故命题正确.
”表示的平面区域为△ABC,不等式“|2y-x|≤2”表示的平面区域为两条平行直线l和m之间的部分,前者为后者的真子集,故命题正确.
故答案为:①②④.
点评:本题考查必要条件、充分条件和充要条件的判断,解题时要认真审题,注意函数的对称性、奇偶性、单调性和可行域的灵活运用.

练习册系列答案
相关题目
 ,平面
,平面 ,若
,若
 ,是
,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件; 为奇函数,则
为奇函数,则
 ,则
,则 为极大值或极小值
为极大值或极小值 的图象的一个对称中心是(
的图象的一个对称中心是( ,0)
,0)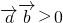 ,是
,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;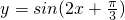 的图象的一个对称中心是
的图象的一个对称中心是
 ,平面
,平面 ,若
,若
 ,是
,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件; 为奇函数,则
为奇函数,则
 ,则
,则 为极大值或极小值
为极大值或极小值 的图象的一个对称中心是(
的图象的一个对称中心是( ,0)
,0)