题目内容
【题目】【2017山西三区八校二模】已知函数![]() (其中
(其中![]() ,
, ![]() 为常数且
为常数且![]() )在
)在![]() 处取得极值.
处取得极值.
(Ⅰ)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 在
在![]() 上的最大值为1,求
上的最大值为1,求![]() 的值.
的值.
【答案】(Ⅰ)单调递增区间为![]() ,
, ![]() ;单调递减区间为
;单调递减区间为![]() ; (Ⅱ)
; (Ⅱ)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)由函数的解析式,可求出函数导函数的解析式,进而根据![]() 是
是![]() 的一个极值点
的一个极值点![]() ,可构造关于
,可构造关于![]() ,
, ![]() 的方程,根据
的方程,根据![]() 求出
求出![]() 值;可得函数导函数的解析式,分析导函数值大于0和小于0时,
值;可得函数导函数的解析式,分析导函数值大于0和小于0时, ![]() 的范围,可得函数
的范围,可得函数![]() 的单调区间;
的单调区间;
(Ⅱ)对函数求导,写出函数的导函数等于0的![]() 的值,列表表示出在各个区间上的导函数和函数的情况,做出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于
的值,列表表示出在各个区间上的导函数和函数的情况,做出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于![]() 的方程求得结果.
的方程求得结果.
试题解析:
(Ⅰ)因为![]() ,所以
,所以![]() ,
,
因为函数![]() 在
在![]() 处取得极值,
处取得极值,
![]()
当![]() 时,
时, ![]() ,
, ![]() ,
,
由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ,
,
即函数![]() 的单调递增区间为
的单调递增区间为![]() ,
, ![]() ;单调递减区间为
;单调递减区间为![]() .
.
(Ⅱ)因为![]() ,
,
令![]() ,
, ![]() ,
, ![]() ,
,
因为![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() 上单调递减,
上单调递减, ![]() 上单调递增,
上单调递增,
所以最大值1可能的在![]() 或
或![]() 处取得,而
处取得,而![]()
![]()
![]() ,
,
所以![]() ,解得
,解得![]() ;
;
当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,
上单调递增, ![]() 上单调递减,
上单调递减, ![]() 上单调递增,
上单调递增,
所以最大值1可能在![]() 或
或![]() 处取得,
处取得,
而![]() ,
,
所以![]() ,
,
解得![]() ,与
,与![]() 矛盾.
矛盾.
当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所最大值1可能在![]() 处取得,而
处取得,而![]() ,矛盾.
,矛盾.
综上所述, ![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案【题目】【2017湖南长沙二模】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
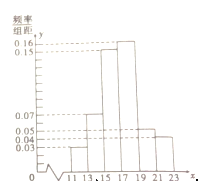
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:

(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?