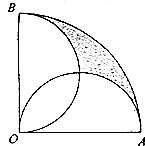题目内容
【题目】设直线系M：xcosθ+ysinθ=1，对于下列四个命题：
①不在直线系M中的点都落在面积为π的区域内
②直线系M中所有直线为一组平行线
③直线系M中所有直线均经过一个定点
④对于任意整数n（n≥3），存在正n边形，其所有边均在直线系M中的直线上
其中真命题的代号是（写出所有真命题的代号）．
【答案】①④
【解析】解：直线M：xcosθ+ysinθ=1，则点（0，0）到直线的距离d= 
=1．
因此直线系表示的是x2+y2=1的圆的所有切线，据此可以判断：
①满足条件的点的圆的面积为π，正确．
②不正确．
③M中所有直线均过一个定点，不正确；
④对于任意正整数n（n≥3），由于上述给出的圆有外切正多边形，因此存在正n边形其所有边均在M中直线上，正确．
综上可得：正确的命题是①④．①④
【考点精析】本题主要考查了一般式方程的相关知识点，需要掌握直线的一般式方程：关于
的二元一次方程
（A，B不同时为0）才能正确解答此题．
阅读快车系列答案
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查，如表是在某单位得到的数据（人数）：
（1）能否有90%以上的把握认为对这一问题的看法与性别有关？
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
（2）从赞同“男女延迟退休”16人中选出3人进行陈 述发言，求事件“男士和女士各至少有1人发言”的概率；
（3）若以这25人的样本数据来估计整个地区的总体数据，现从该地区（人数很多）任选5人，记赞同“男女延迟退休”的人数为X，求X的数学期望．
附：
p（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= 
．
【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响，某农科所记录了5组昼夜温差与100颗种子发芽数，得到如表资料：
组号 | 1 | 2 | 3 | 4 | 5 |
温差x（°C） | 10 | 11 | 13 | 12 | 8 |
发芽数y（颗） | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求出线性回归方程，再对被选取的2组数据进行检验．
（1）若选取的是第1组与第5组的两组数据，请根据第2组至第4组的数据，求出y关于x的线性回归方程 
；
（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？
（参考公式： 
= 
= 
， 
）
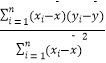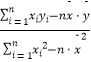