题目内容
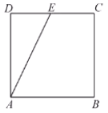
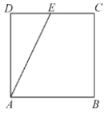
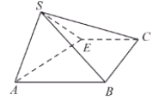
【题目】如图,点![]() 为正方形
为正方形![]() 边
边![]() 上异于点
上异于点![]() ,
,![]() 的动点,将
的动点,将![]() 沿
沿![]() 翻折成
翻折成![]() ,在翻折过程中,下列说法正确的是( )
,在翻折过程中,下列说法正确的是( )
A.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]()
B.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]() 平面
平面![]()
C.存在点![]() 和某一翻折位置,使得直线
和某一翻折位置,使得直线![]() 与平面
与平面![]() 所成的角为45°
所成的角为45°
D.存在点![]() 和某一翻折位置,使得二面角
和某一翻折位置,使得二面角![]() 的大小为60°
的大小为60°
【答案】ACD
【解析】
依次判断每个选项:当![]() 时,
时,![]() ,
,![]() 正确,
正确,![]() 平面
平面![]() ,则
,则![]() ,这与已知矛盾,故
,这与已知矛盾,故![]() 错误,取二面角
错误,取二面角![]() 的平面角为
的平面角为![]() ,取
,取![]() ,计算得到
,计算得到![]() ,
,![]() 正确,取二面角
正确,取二面角![]() 的平面角为
的平面角为![]() ,计算得到
,计算得到![]() ,故
,故![]() 正确,得到答案.
正确,得到答案.
当![]() 时,
时,![]() ,
,![]() ,故
,故![]() 平面
平面![]() ,故
,故![]() ,
,![]() 正确;
正确;
若![]() 平面
平面![]() ,因
,因![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,则
,则![]() ,
,
这与已知矛盾,故![]() 错误;
错误;
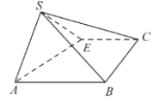
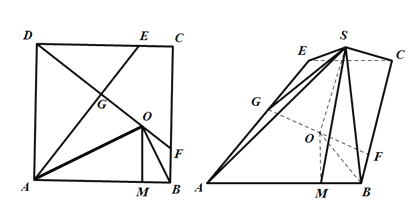
如图所示:![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 在平面
在平面![]() 的投影
的投影![]() 在
在![]() 上,
上,
连接![]() ,故
,故![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
取二面角![]() 的平面角为
的平面角为![]() ,取
,取![]() ,
,![]() ,故
,故![]() ,
,
![]() ,
,![]() ,
,![]() ,故只需满足
,故只需满足![]() ,
,
在![]() 中,根据余弦定理:
中,根据余弦定理:
![]() ,解得
,解得![]() ,故
,故![]() 正确;
正确;
过![]() 作
作![]() 交
交![]() 于
于![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
取二面角![]() 的平面角为
的平面角为![]() ,故只需满足
,故只需满足![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
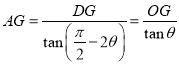 ,化简得到
,化简得到![]() ,解得
,解得![]() ,验证满足,故
,验证满足,故![]() 正确;
正确;
故选:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
|
|
|
|
环保部门对企业评估完成后,随机抽取了![]() 家企业的评估得分(
家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是
表示模糊不清的两个数字,但知道样本评估得分的平均数是![]() .
.
(1)现从样本外的数百个企业评估得分中随机抽取![]() 个,若以样本中频率为概率,求该家企业的奖励不少于
个,若以样本中频率为概率,求该家企业的奖励不少于![]() 万元的概率;
万元的概率;
(2)现从样本“不合格”、“合格”、“良好”三个等级中,按分层抽样的方法抽取![]() 家企业,再从这
家企业,再从这![]() 家企业随机抽取
家企业随机抽取![]() 家,求这两家企业所获奖励之和不少于
家,求这两家企业所获奖励之和不少于![]() 万元的概率.
万元的概率.