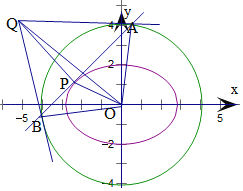
题目内容
【题目】已知直线
与椭圆
切于点
，与圆
交于点
，圆
在点处的切线交于点
，
为坐标原点，则
的面积的最大值为（ ）
A.
B.2C.
D.1
【答案】A
【解析】
设点
，
，利用四点
，
，
，
共圆，求得以
为直径的圆，与已知圆的方程相减得出直线
的方程，直线与过点
的椭圆的切线重合，两个方程相等，可得
,
，再由椭圆的参数方程和向量数量积的坐标表示和向量的模，结合三角形的面积公式和三角恒等变换以及三角函数的基本性质求出所求的最大值。
设
，
，
，由
，
，可得四点，，，共圆，
可得以为直径的圆，方程为
，
联立圆
，相减可得的方程为
，
又与椭圆相切，可得过的切线方程为
，即为
，
由两直线重合的条件可得，，
由于在椭圆上，可设
，
，
，
即有
，
，
可得
，
且
，
，
即有
，
，当
即
或
或
或
时，
的面积取得最大值
．
故选：．
练习册系列答案
相关题目
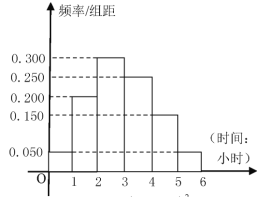
【题目】某校共有学生2000人，其中男生1100人，女生900人为了调查该校学生每周平均课外阅读时间，采用分层抽样的方法收集该校100名学生每周平均课外阅读时间（单位：小时）
（1）应抽查男生与女生各多少人？
（2）如图，根据收集100人的样本数据，得到学生每周平均课外阅读时间的频率分布直方图，其中样本数据分组区间为
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时，请完成每周平均课外阅读时间与性别的列联表，并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附：
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
