题目内容
设数{an}的前n项和为Sn=4-| 1 | 4n-1 |
(I)求数列{an}、{bn}的通项公式;
(II)设cn=anbn,求数列{cn}的前n项和Tn.
分析:(I)根据an=sn-sn-1,求出数列{an}的通项公式;由a2(b2-b1)=a1,求出b2、b1,进而求出公差,再由等差数列得到数列{bn}的通项公式;
(II)首先由(I)得出求数列{cn}的通项公式,然后求出4Tn-Tn,进而求出前n项和Tn.
(II)首先由(I)得出求数列{cn}的通项公式,然后求出4Tn-Tn,进而求出前n项和Tn.
解答:解(Ⅰ)由数列{an}的前n项和为Sn=4-
得:an=Sn-Sn-1=4-
-4+
=
(n≥2)
a1=S1=4-1=3(n=1)
∴an=
(n∈N*)(3分)
b1=a1=3,a2(b2-b1)=a1?
(b2-b1)=3∴b2-b1=4
数列{bn}为等差数列,
所以bn=b1+(n-1)4=4n-1(16分)
(Ⅱ)设cn=anbn=
Tn=
+
++
+
①4Tn=4•
+
+
+
②(9分)
②-①3Tn=4×9+3×4(
+
++
+
)-
Tn=
-
-
或
-
或
-
-
(12分)
| 1 |
| 4n-1 |
得:an=Sn-Sn-1=4-
| 1 |
| 4n-1 |
| 1 |
| 4n-2 |
| 3 |
| 4n-1 |
a1=S1=4-1=3(n=1)
∴an=
| 3 |
| 4n-1 |
b1=a1=3,a2(b2-b1)=a1?
| 3 |
| 4 |
数列{bn}为等差数列,
所以bn=b1+(n-1)4=4n-1(16分)
(Ⅱ)设cn=anbn=
| 3(4n-1) |
| 4n-1 |
| 3×3 |
| 1 |
| 3×7 |
| 4 |
| 3(4n-5) |
| 4n-1 |
| 3(4n-1) |
| 4n-1 |
| 3×3 |
| 1 |
| 3×7 |
| 1 |
| 3×11 |
| 41 |
| 3(4n-5) |
| 4n-3 |
| 3(4n-1) |
| 4n-2 |
②-①3Tn=4×9+3×4(
| 1 |
| 1 |
| 1 |
| 41 |
| 1 |
| 4n-3 |
| 1 |
| 4n-2 |
| 3(4n-1) |
| 4n-1 |
| 52 |
| 3 |
| 1 |
| 3•4n-3 |
| (4n-1) |
| 4n-1 |
| 52 |
| 3 |
| 48n+52 |
| 3•4n |
| 52 |
| 3 |
| n |
| 4n-2 |
| 13 |
| 3•4n-1 |
点评:本题考查数列的递推式、等差数列的通项公式以及数列的前n项和,对于等差数列和等比数列乘积形式的数列一般采取错位相减的方法求前n项和,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
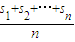 ,称Tn为数a1,a2,…an 的“理想数”,已知数a1,a2,…a500的“理想数”为2004,那么数列8,a1,a2,…a500的“理想数”为( )
,称Tn为数a1,a2,…an 的“理想数”,已知数a1,a2,…a500的“理想数”为2004,那么数列8,a1,a2,…a500的“理想数”为( )