题目内容
设数{an}的前n项和为Sn,若对任意的n∈N*,有an>0且 2Sn=
+an成立.
(1)求a1、a2的值;
(2)求数列{an}的通项公式an;
(3)设数列{an}的前n项和为Sn,令Tn=
,若数列{Tn}为单调递增数列,求实数c的取值范围.
| a | 2 n |
(1)求a1、a2的值;
(2)求数列{an}的通项公式an;
(3)设数列{an}的前n项和为Sn,令Tn=
| Sn |
| cn |
分析:(1)根据对任意的n∈N*,有an>0且 2Sn=
+an成立,分别令n=1和n=2,能求出a1,a2的值.
(2)由2Sn=
+an,得2Sn+1=an+12+an+1,两式作差可得an+1-an-1=0,由此能求出数列{an}的通项公式an.
(3)由an=n,得Sn=
,故Tn+1-Tn=
-
=
(n+2-cn),由此进行等价转化,能够求出实数c的取值范围.
| a | 2 n |
(2)由2Sn=
| a | 2 n |
(3)由an=n,得Sn=
| n(n+1) |
| 2 |
| (n+1)(n+2) |
| 2•cn+1 |
| n(n+1) |
| 2•cn |
| n+1 |
| 2•cn+1 |
解答:解:(1)∵对任意的n∈N*,有an>0且 2Sn=
+an成立,
∴2S1=2a1=a12+a1,
即a12-a1=0,
解得a1=0(舍),a1=1.…(2分)
2S2=2(1+a2)=a22+a2,
整理,得a22-a2-2=0,
解得a2=-1(舍),a2=2.…(4分)
(2)∵2Sn=
+an,
∴2Sn+1=an+12+an+1,
两式作差可得2Sn+1-2Sn=2an+1=an+12+an+1-an2-(an+1+an)=0,
∴(an+1+an)(an+1-an-1)=0,…(6分)
因为an>0,所以an+1+an>0,
∴an+1-an-1=0,…(8分)
所以数列{an}为等差数列,…(9分)
首项a1=1,公差为1,所以an=n;…(10分)
(3)∵an=n,∴Sn=
,…(11分)
∴Tn+1-Tn=
-
=
(n+2-cn),…(12分)
数列{Tn}为单调递增数列,
当且仅当Tn+1-Tn>0?n+2-cn>0?c<
=1+
恒成立,…(14分)
即c≤1,…(15分)
显然c>0,综上所述c∈(0,1].…(16分)
| a | 2 n |
∴2S1=2a1=a12+a1,
即a12-a1=0,
解得a1=0(舍),a1=1.…(2分)
2S2=2(1+a2)=a22+a2,
整理,得a22-a2-2=0,
解得a2=-1(舍),a2=2.…(4分)
(2)∵2Sn=
| a | 2 n |
∴2Sn+1=an+12+an+1,
两式作差可得2Sn+1-2Sn=2an+1=an+12+an+1-an2-(an+1+an)=0,
∴(an+1+an)(an+1-an-1)=0,…(6分)
因为an>0,所以an+1+an>0,
∴an+1-an-1=0,…(8分)
所以数列{an}为等差数列,…(9分)
首项a1=1,公差为1,所以an=n;…(10分)
(3)∵an=n,∴Sn=
| n(n+1) |
| 2 |
∴Tn+1-Tn=
| (n+1)(n+2) |
| 2•cn+1 |
| n(n+1) |
| 2•cn |
| n+1 |
| 2•cn+1 |
数列{Tn}为单调递增数列,
当且仅当Tn+1-Tn>0?n+2-cn>0?c<
| n+2 |
| n |
| 2 |
| n |
即c≤1,…(15分)
显然c>0,综上所述c∈(0,1].…(16分)
点评:本题考查数列的首项和第二项的求法,考查数列通项公式的求法,考查实数的取值范围的求法.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
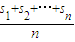 ,称Tn为数a1,a2,…an 的“理想数”,已知数a1,a2,…a500的“理想数”为2004,那么数列8,a1,a2,…a500的“理想数”为( )
,称Tn为数a1,a2,…an 的“理想数”,已知数a1,a2,…a500的“理想数”为2004,那么数列8,a1,a2,…a500的“理想数”为( )