题目内容
设数{an}的前n项和sn,Tn=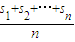 ,称Tn为数a1,a2,…an 的“理想数”,已知数a1,a2,…a500的“理想数”为2004,那么数列8,a1,a2,…a500的“理想数”为( )
,称Tn为数a1,a2,…an 的“理想数”,已知数a1,a2,…a500的“理想数”为2004,那么数列8,a1,a2,…a500的“理想数”为( )A.2008
B.2009
C.2010
D.2011
【答案】分析:利用“理想数”的定义即可得到a1+(a1+a2)+…+(a1+a2+…+a500)=500×2004,进而即可得到数列8,a1,a2,…a500的“理想数”.
解答:解:∵数a1,a2,…a500的“理想数”为2004,∴2004=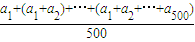 ,∴a1+(a1+a2)+…+(a1+a2+…+a500)=500×2004.
,∴a1+(a1+a2)+…+(a1+a2+…+a500)=500×2004.
∴数列8,a1,a2,…a500的“理想数”=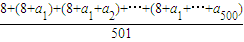 =8+
=8+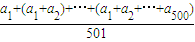
=8+ =8+2000=2008.
=8+2000=2008.
故选A.
点评:正确理解“理想数”的定义和具有较强的计算能力是解题的关键.
解答:解:∵数a1,a2,…a500的“理想数”为2004,∴2004=
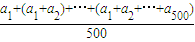 ,∴a1+(a1+a2)+…+(a1+a2+…+a500)=500×2004.
,∴a1+(a1+a2)+…+(a1+a2+…+a500)=500×2004.∴数列8,a1,a2,…a500的“理想数”=
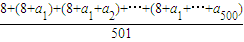 =8+
=8+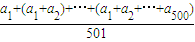
=8+
 =8+2000=2008.
=8+2000=2008.故选A.
点评:正确理解“理想数”的定义和具有较强的计算能力是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目