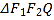ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΨΌ––ΒΡΓΑ»ΐ…Ϊ«ρΓ±ΙΚΈοΟΰΫ±ΜνΕ·ΙφΕ®ΘΚ‘Ύ“Μ¥ΈΟΰΫ±÷–Θ§ΟΰΫ±’Ώœ»¥”ΉΑ”–3ΗωΚλ«ρ”κ4ΗωΑΉ«ρΒΡ¥ϋ÷–»Έ“βΟΰ≥ω3Ηω«ρΘ§‘Ό¥”ΉΑ”–1ΗωάΕ«ρ”κ2ΗωΑΉ«ρΒΡ¥ϋ÷–»Έ“βΟΰ≥ω1Ηω«ρΘ§ΗυΨίΟΰ≥ω4Ηω«ρ÷–Κλ«ρ”κάΕ«ρΒΡΗω ΐΘ§…η“ΜΓΔΕΰΓΔ»ΐΒ»Ϋ±»γœ¬ΘΚ
Ϋ±ΦΕ | Οΰ≥ωΚλΓΔάΕ«ρΗω ΐ | ΜώΫ±ΫπΕν |
“ΜΒ»Ϋ± | 3Κλ1άΕ | 200‘Σ |
ΕΰΒ»Ϋ± | 3Κλ0άΕ | 50‘Σ |
»ΐΒ»Ϋ± | 2Κλ1άΕ | 10‘Σ |
Τδ”ύ«ιΩωΈόΫ±«“ΟΩ¥ΈΟΰΫ±ΉνΕύ÷ΜΡήΜώΒΟ“ΜΗωΫ±ΦΕ.
Θ®1Θ©«σΟΰΫ±’ΏΒΎ“Μ¥ΈΟΰ«ρ ±«ΓΚΟΟΰΒΫ1ΗωΚλ«ρΒΡΗ≈¬ ΘΜ
Θ®2Θ©«σΟΰΫ±’Ώ‘Ύ“Μ¥ΈΟΰΫ±÷–ΜώΫ±ΫπΕν![]() ΒΡΖ÷≤ΦΝ–.
ΒΡΖ÷≤ΦΝ–.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©œξΦϊΫβΈω.
ΘΜΘ®2Θ©œξΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©¥”ΉΑ”–3ΗωΚλ«ρ”κ4ΗωΑΉ«ρΒΡ¥ϋ÷–»Έ“βΟΰ≥ω3Ηω«ρΘ§”–![]() ÷÷ΖΫΖ®Θ§«ΓΚΟΟΰΒΫ1ΗωΚλ«ρ”–
÷÷ΖΫΖ®Θ§«ΓΚΟΟΰΒΫ1ΗωΚλ«ρ”–![]() ÷÷ΖΫΖ®Θ§»ΜΚσΩ…«σΗ≈¬ ΘΜ
÷÷ΖΫΖ®Θ§»ΜΚσΩ…«σΗ≈¬ ΘΜ
Θ®2Θ©«σ≥ω![]() ΒΡΥυ”–Ω…Ρή÷ΒΘ§Ζ÷±π«σΫβΤδΕ‘”ΠΒΡΗ≈¬ Θ§»ΜΚσΩ…ΒΟΖ÷≤ΦΝ–.
ΒΡΥυ”–Ω…Ρή÷ΒΘ§Ζ÷±π«σΫβΤδΕ‘”ΠΒΡΗ≈¬ Θ§»ΜΚσΩ…ΒΟΖ÷≤ΦΝ–.
…η![]() ±μ ΨΟΰΒΫ
±μ ΨΟΰΒΫ![]() ΗωΚλ«ρΘ§
ΗωΚλ«ρΘ§![]() ±μ ΨΟΰΒΫ
±μ ΨΟΰΒΫ![]() ΗωάΕ«ρΘ§‘ρ
ΗωάΕ«ρΘ§‘ρ![]() ”κ
”κ![]() ΕάΝΔ.
ΕάΝΔ.
Θ®1Θ©¥”ΉΑ”–3ΗωΚλ«ρ”κ4ΗωΑΉ«ρΒΡ¥ϋ÷–»Έ“βΟΰ≥ω3Ηω«ρΘ§”–![]() ÷÷ΖΫΖ®Θ§«ΓΚΟΟΰΒΫ1ΗωΚλ«ρ”–
÷÷ΖΫΖ®Θ§«ΓΚΟΟΰΒΫ1ΗωΚλ«ρ”–![]() ÷÷ΖΫΖ®Θ§Ι Υυ«σΗ≈¬ ΈΣ
÷÷ΖΫΖ®Θ§Ι Υυ«σΗ≈¬ ΈΣ![]() .
.
Θ®2Θ©![]() ΒΡΥυ”–Ω…Ρή÷ΒΈΣΘΚ0Θ§10Θ§50Θ§200Θ§«“
ΒΡΥυ”–Ω…Ρή÷ΒΈΣΘΚ0Θ§10Θ§50Θ§200Θ§«“
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() .
.
Ήέ…œ÷Σ![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
| 0 | 10 | 50 | 200 |
|
|
|
|
|