题目内容
体积为52的圆台，一个底面积是另一个底面积的9倍，那么截得这个圆台的圆锥的体积是______．
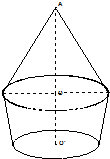
如图所示，将圆台补成圆锥，则图中小圆锥与大圆锥是相似的几何体
设大、小圆锥的底面半径分别为r、R，高分别为h、H
∵圆台上、下底面的面积之比为1：9，
∴小圆锥与大圆锥的相似比为1：3，即半径之比
=
且高之比
=
因此，小圆锥与大圆锥的体积之比
=（
）3=
，
可得
=1-
=
，
因此，截得这个圆台的圆锥体积和圆台体积之比27：26，
又圆台的体积为52cm3，则截该圆台的圆锥体积为
×52=54．
故答案为：54．
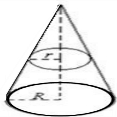
设大、小圆锥的底面半径分别为r、R，高分别为h、H
∵圆台上、下底面的面积之比为1：9，
∴小圆锥与大圆锥的相似比为1：3，即半径之比
| r |
| R |
| 1 |
| 3 |
| h |
| H |
| 1 |
| 3 |
因此，小圆锥与大圆锥的体积之比
| V小 |
| V大 |
| 1 |
| 3 |
| 1 |
| 27 |
可得
| V圆台 |
| V大 |
| 1 |
| 27 |
| 26 |
| 27 |
因此，截得这个圆台的圆锥体积和圆台体积之比27：26，
又圆台的体积为52cm3，则截该圆台的圆锥体积为
| 27 |
| 26 |
故答案为：54．
练习册系列答案
相关题目
