题目内容
观察下面两个推理过程及结论:
(1) 若锐角A, B, C满足A+B+C= , 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式:
, 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式: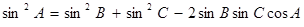
(2) 若锐角A, B, C满足A+B+C= , 则
, 则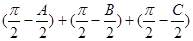 =
= , 以
, 以  分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
得到的等式: 则:若锐角A, B, C满
则:若锐角A, B, C满
足A+B+C= , 类比上面推理方法, 可以得到一个等式是 .
, 类比上面推理方法, 可以得到一个等式是 .
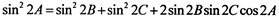
解析试题分析:根据题意,由于锐角A, B, C满足A+B+C= , 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式:
, 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式: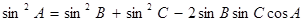 ,锐角A, B, C满
,锐角A, B, C满
足A+B+C= , 类比上面推理方法,
, 类比上面推理方法, 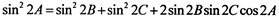 ,故答案为
,故答案为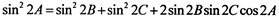 。
。
考点:类比推理
点评:主要是考查了类比推理的运用,属于基础题。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
 内植树,第一棵树在点Al(0,1),第二棵树在点.B1(l,l),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么
内植树,第一棵树在点Al(0,1),第二棵树在点.B1(l,l),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么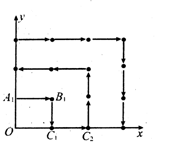
 ,计算
,计算 ,
, ,推测当
,推测当 时,有_____________.
时,有_____________.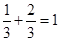 ;
; ;
; ;……
;…… 且
且 时,
时, .(最后结果用
.(最后结果用 表示).
表示).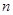 条两两相交的弦,把圆最多分成 部分.
条两两相交的弦,把圆最多分成 部分.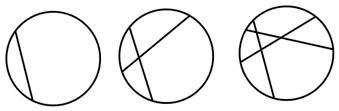
 cr、
cr、 ,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________. 个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为 .
个小球,将它们任意分成两堆,求出这两堆小球球数的乘积,再将其中一堆小球任意分成两堆,求出这两堆小球球数的乘积,如此下去,每次都任选一堆,将这堆小球任意分成两堆,求出这两堆小球球数的乘积,直到不能再分为止,则所有乘积的和为 . ,
, ,
, ,…,
,…,