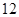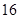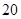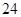题目内容
(本题13分)已知数列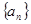 满足a1=0,a2=2,且对任意m,
满足a1=0,a2=2,且对任意m,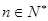 都有
都有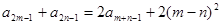
(1)求a3,a5;
(2)求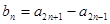
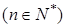 ,证明:
,证明: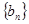 是等差数列;
是等差数列;
(3)设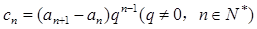 ,求数列
,求数列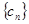 的前n项和Sn。
的前n项和Sn。
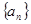 满足a1=0,a2=2,且对任意m,
满足a1=0,a2=2,且对任意m,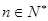 都有
都有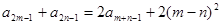
(1)求a3,a5;
(2)求
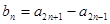
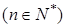 ,证明:
,证明: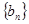 是等差数列;
是等差数列;(3)设
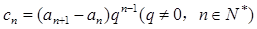 ,求数列
,求数列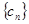 的前n项和Sn。
的前n项和Sn。(1)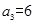 ,
,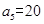 ;(2)见解析;
;(2)见解析;
(3)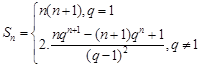
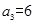 ,
,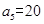 ;(2)见解析;
;(2)见解析;(3)
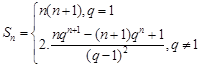
本题考查等差等比数列的证明和数列的求和,利用错位相减法求和的时,注意讨论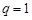 与
与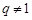 的两种情形以及相减以后项数的确定。
的两种情形以及相减以后项数的确定。
解:(1)由题意,令m=2,n=1可得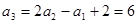 。
。
再令m=3,n=1可得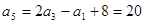 . (2分)
. (2分)
(2)当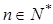 时,由已知(以n+2代替m)可得
时,由已知(以n+2代替m)可得
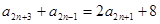
于是,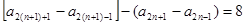 即
即
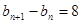 。
。
所以,数列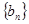 是首项
是首项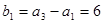 ,公差为8的等差数列。 (5分)
,公差为8的等差数列。 (5分)
(3)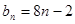 ,则
,则 。
。
另由已知(令m=1)可得,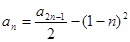
那么,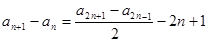
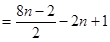
=2n
于是,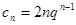
当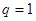 时,
时,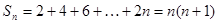 。
。
当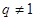 时,
时,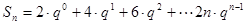
两边同乘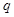 可得
可得
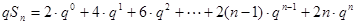
上述两式相减即得
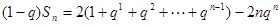
=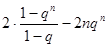
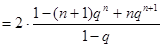
所以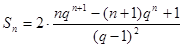
综上所述,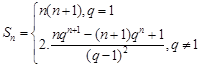
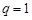 与
与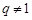 的两种情形以及相减以后项数的确定。
的两种情形以及相减以后项数的确定。解:(1)由题意,令m=2,n=1可得
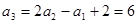 。
。再令m=3,n=1可得
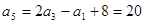 . (2分)
. (2分)(2)当
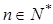 时,由已知(以n+2代替m)可得
时,由已知(以n+2代替m)可得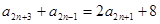
于是,
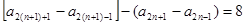 即
即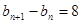 。
。所以,数列
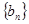 是首项
是首项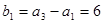 ,公差为8的等差数列。 (5分)
,公差为8的等差数列。 (5分)(3)
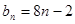 ,则
,则 。
。另由已知(令m=1)可得,
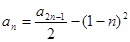
那么,
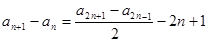
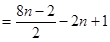
=2n
于是,
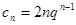
当
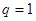 时,
时,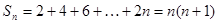 。
。当
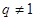 时,
时,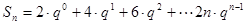
两边同乘
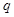 可得
可得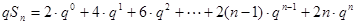
上述两式相减即得
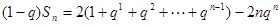
=
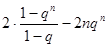
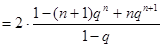
所以
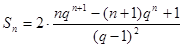
综上所述,

练习册系列答案
相关题目
 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第 个1和第
个1和第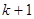 个1之间有
个1之间有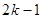 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前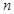 项的和为
项的和为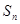 .
.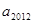 和
和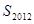 ;
;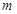 ,使得
,使得 ?如果存在,求出
?如果存在,求出 的前
的前 项和为
项和为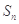 ,等比数列
,等比数列 的各项均为正数,公比是
的各项均为正数,公比是 ,且满足:
,且满足: .
.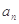 与
与 ;
; ,若
,若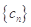 满足:
满足: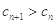 对任意的
对任意的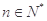 恒成立,求
恒成立,求 的取值范围.
的取值范围.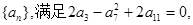 数列
数列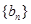 是等比数列,且
是等比数列,且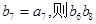 = ( )
= ( ) 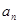 }的前n项和为Sn,且
}的前n项和为Sn,且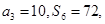 bn=
bn=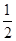
 的前n项和为
的前n项和为 ,
,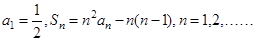
 是等差数列,并求
是等差数列,并求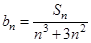 ,求证:
,求证: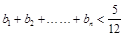 .
.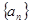 是等差数列,且
是等差数列,且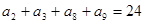 ,则
,则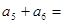 ( )
( )