题目内容
已知函数
(1)当
时，求
上的最大值、最小值：
(2)求
的单调区间；
【答案】
略
【解析】
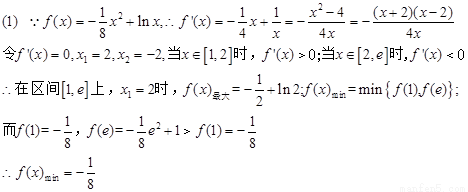
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案芒果教辅暑假天地重庆出版社系列答案题目内容
已知函数
(1)当时，求上的最大值、最小值：
(2)求的单调区间；
略
【解析】
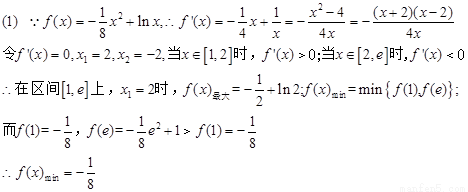
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案芒果教辅暑假天地重庆出版社系列答案
.
时，讨论
的单调性；
当
时，若对任意
，存在
，使
恒成立，求实数
取值范围.
时, 证明: 不等式
恒成立; 
满足
,证明数列
是等比数列,并求出数列
，证明：
.
时，求函数
的最值；
使
的图象与
无公共点.
,
时,求函数
的单调递增区间;
2,0]上不单调,且
时,不等式
恒成立,求实数a的取值范围.
时，求函数
的最小值；
使
的图象与
无公共点.