题目内容
(本小题满分12分)
已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),α∈( ,
, ).
).
(1)若| |=|
|=| |,求角α的值;
|,求角α的值;
(2)若 ·
· =-1,求
=-1,求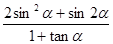 的值.
的值.
已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),α∈(
 ,
, ).
).(1)若|
 |=|
|=| |,求角α的值;
|,求角α的值;(2)若
 ·
· =-1,求
=-1,求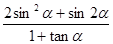 的值.
的值.(1)α= .(2)
.(2)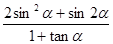 =
=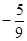 .
.
 .(2)
.(2)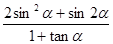 =
=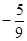 .
.本试题主要是考查了向量的数量积公式和三角函数的化简求值的综合运用。
(1)由| |=|
|=| |,得sinα=cosα.
|,得sinα=cosα.
然后得到角的值。
(2)根据由 ·
· =-1,得(cosα-3)cosα+sinα(sinα-3)=-1.
=-1,得(cosα-3)cosα+sinα(sinα-3)=-1.
∴sinα+cosα= ,化简已知关系式,得到结论。
,化简已知关系式,得到结论。
解:(1)∵ =(cosα-3,sinα),
=(cosα-3,sinα), =(cosα,sinα-3),
=(cosα,sinα-3),
∴| |=
|= ,
,
| |=
|= .
.
由| |=|
|=| |,得sinα=cosα.
|,得sinα=cosα.
又∵α∈( ,
,  ),∴α=
),∴α= .
.
(2)由 ·
· =-1,得(cosα-3)cosα+sinα(sinα-3)=-1.
=-1,得(cosα-3)cosα+sinα(sinα-3)=-1.
∴sinα+cosα= .①
.①
又 =2sinαcosα.
=2sinαcosα.
由①式两边平方,得1+2sinαcosα= ,
,
∴2sinαcosα=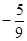 .∴
.∴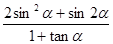 =
=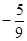 .
.
(1)由|
 |=|
|=| |,得sinα=cosα.
|,得sinα=cosα.然后得到角的值。
(2)根据由
 ·
· =-1,得(cosα-3)cosα+sinα(sinα-3)=-1.
=-1,得(cosα-3)cosα+sinα(sinα-3)=-1.∴sinα+cosα=
 ,化简已知关系式,得到结论。
,化简已知关系式,得到结论。解:(1)∵
 =(cosα-3,sinα),
=(cosα-3,sinα), =(cosα,sinα-3),
=(cosα,sinα-3),∴|
 |=
|= ,
,|
 |=
|= .
.由|
 |=|
|=| |,得sinα=cosα.
|,得sinα=cosα.又∵α∈(
 ,
,  ),∴α=
),∴α= .
.(2)由
 ·
· =-1,得(cosα-3)cosα+sinα(sinα-3)=-1.
=-1,得(cosα-3)cosα+sinα(sinα-3)=-1.∴sinα+cosα=
 .①
.①又
 =2sinαcosα.
=2sinαcosα.由①式两边平方,得1+2sinαcosα=
 ,
,∴2sinαcosα=
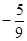 .∴
.∴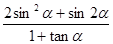 =
=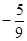 .
.
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
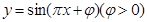 的部分图像如图所示,设
的部分图像如图所示,设 是函数图象的最高点,
是函数图象的最高点, ,
, 是图像与
是图像与 轴的交点,则
轴的交点,则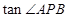 =( )
=( )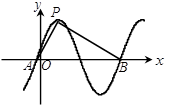


 ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α<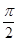 .
.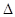 ABC的内角A、B、C的对边分别为a、b、c,cos(A—C)+cos B=
ABC的内角A、B、C的对边分别为a、b、c,cos(A—C)+cos B=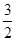 ,b2=ac,求B.
,b2=ac,求B.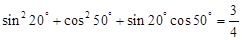 ,
, 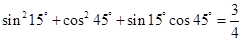
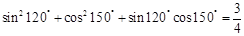 ,根据其共同特点,写出能反映一般规律的等式
,根据其共同特点,写出能反映一般规律的等式 则
则 ( )
( )



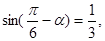 则
则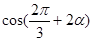 的值是 .
的值是 . ,则
,则 的值为
的值为



 ,那么
,那么 = .
= .