��Ŀ����
������{an}��{bn}�У�an=an��bn=��a+1��n+b��n=1��2��3����������a��2��a��N*��b��R��������a1=b1��a2��b2��������{bn}��ǰn��ͣ�
����֤������
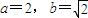 ʱ������{bn}�е�����������ܹ��ɵȱ����У�
ʱ������{bn}�е�����������ܹ��ɵȱ����У�������A={a1��a2��a3����}��B={b1��b2��b3����}������������[1��a]���Ƿ����ʵ��bʹ��C=A��B��∅�������ڣ����b��һ�п��ܵ�ȡֵ����Ӧ�ļ���C���������ڣ���˵�����ɣ�
���𰸡���������I����a1=b1��a2��b2�������֪�ɽ���a��b�ķ��̣��Ӷ�����a��b����һ���������bn��ͨ�ǰn���
��II�� ��ϣ�I��֪
��ϣ�I��֪ ������amanat��m��n��t��N+���ɵȱ����У���m��n��t���ɼ����Ƶ��ɵ�
������amanat��m��n��t��N+���ɵȱ����У���m��n��t���ɼ����Ƶ��ɵ�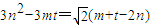 �����m��t��n��N+��������֪ì�ܣ�
�����m��t��n��N+��������֪ì�ܣ�
��III�������ʵ��b��[1��a]��ʹC=A��B��∅����m��C����m��A����m��B��
��m��A����m=at����m��B����mo=��a+1��s+b�������ɵ�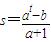 ��tΪ��ż����ֱ�������ۣ����Ƴ�ì�ܣ���˵�������ڣ�������ڷ���������ʵ��b
��tΪ��ż����ֱ�������ۣ����Ƴ�ì�ܣ���˵�������ڣ�������ڷ���������ʵ��b
����⣺������Ϊa1=b1������a=a+1+b��b=-1����1�֣�
��a2��b2����a2-2a-1��0��
����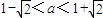 ����3�֣�
����3�֣�
��Ϊa��2��a��N*������a=2����4�֣�
����bn=3n-1��{bn}�ǵȲ����У�
��������{bn}��ǰn���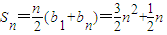 ����5�֣�
����5�֣�
��������֪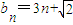 ������
������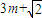 ��
��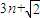 ��
��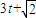 �ɵȱ����У�����m��n��t��N*���ұ˴˲��ȣ�
�ɵȱ����У�����m��n��t��N*���ұ˴˲��ȣ�
��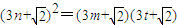 ����6�֣�
����6�֣�
����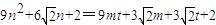 ��
��
����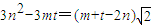 ��
��
��m+t-2n=0����3n2-3mt=0���ɵ�m=t����m��tì�ܣ���7�֣�
��m+t-2n��0����m+t-2n����������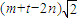 ��������
��������
����3n2-3mtΪ����������3n2-3mt������ì�ܣ���9�֣�
��������{bn}�е�����������ܹ��ɵȱ����У�
���������ʵ��b��[1��a]��ʹC=A��B��∅��
��m��C����m��A����m��B��
��m=at��t��N*����m=��a+1��s+b��s��N*����
��at=��a+1��s+b������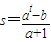 ��
��
��Ϊa��t��s��N*����a��2������at-b�ܱ�a+1��������10�֣�
��1����t=1ʱ����Ϊb��[1��a]��a-b��[0��a-1]��
����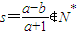 ����11�֣�
����11�֣�
��2����t=2n��n��N*��ʱ��a2n-b=[��a+1��-1]2n-b=��a+1��2n+-C2n1��a+1��+1-b��
����b��[1��a]������b-1��[0��a-1]��0��b-1��a+1��
���ԣ����ҽ���b=1ʱ��at-b�ܱ�a+1��������12�֣�
��3����t=2n+1��n��N*��ʱ��a2n+1-b=[��a+1��-1]2n+1-b=��a+1��2n+1++C2n+11��a+1��-1-b��
����b��[1��a]������b+1��[2��a+1]��
���ԣ����ҽ���b+1=a+1����b=aʱ��at-b�ܱ�a+1��������13�֣�
���ϣ�������[1��a]�ϴ���ʵ��b��ʹC=A��B��∅�������ҵ�b=1ʱ��C={y|y=a2n��n��N*}����b=aʱ��C={y|y=a2n+1��n��N}��
�����������ۺϿ��������е���͡��ȱ����еĶ��塢�����뼯���ۺϣ������˿�����������������������⡢��������������
��II��
 ��ϣ�I��֪
��ϣ�I��֪ ������amanat��m��n��t��N+���ɵȱ����У���m��n��t���ɼ����Ƶ��ɵ�
������amanat��m��n��t��N+���ɵȱ����У���m��n��t���ɼ����Ƶ��ɵ�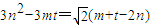 �����m��t��n��N+��������֪ì�ܣ�
�����m��t��n��N+��������֪ì�ܣ���III�������ʵ��b��[1��a]��ʹC=A��B��∅����m��C����m��A����m��B��
��m��A����m=at����m��B����mo=��a+1��s+b�������ɵ�
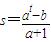 ��tΪ��ż����ֱ�������ۣ����Ƴ�ì�ܣ���˵�������ڣ�������ڷ���������ʵ��b
��tΪ��ż����ֱ�������ۣ����Ƴ�ì�ܣ���˵�������ڣ�������ڷ���������ʵ��b����⣺������Ϊa1=b1������a=a+1+b��b=-1����1�֣�
��a2��b2����a2-2a-1��0��
����
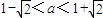 ����3�֣�
����3�֣���Ϊa��2��a��N*������a=2����4�֣�
����bn=3n-1��{bn}�ǵȲ����У�
��������{bn}��ǰn���
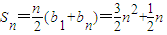 ����5�֣�
����5�֣���������֪
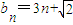 ������
������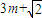 ��
��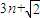 ��
��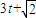 �ɵȱ����У�����m��n��t��N*���ұ˴˲��ȣ�
�ɵȱ����У�����m��n��t��N*���ұ˴˲��ȣ���
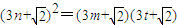 ����6�֣�
����6�֣�����
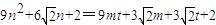 ��
������
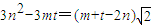 ��
����m+t-2n=0����3n2-3mt=0���ɵ�m=t����m��tì�ܣ���7�֣�
��m+t-2n��0����m+t-2n����������
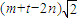 ��������
Ϊ������������3n2-3mtΪ����������3n2-3mt������ì�ܣ���9�֣�
��������{bn}�е�����������ܹ��ɵȱ����У�
���������ʵ��b��[1��a]��ʹC=A��B��∅��
��m��C����m��A����m��B��
��m=at��t��N*����m=��a+1��s+b��s��N*����
��at=��a+1��s+b������
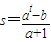 ��
����Ϊa��t��s��N*����a��2������at-b�ܱ�a+1��������10�֣�
��1����t=1ʱ����Ϊb��[1��a]��a-b��[0��a-1]��
����
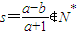 ����11�֣�
����11�֣���2����t=2n��n��N*��ʱ��a2n-b=[��a+1��-1]2n-b=��a+1��2n+-C2n1��a+1��+1-b��
����b��[1��a]������b-1��[0��a-1]��0��b-1��a+1��
���ԣ����ҽ���b=1ʱ��at-b�ܱ�a+1��������12�֣�
��3����t=2n+1��n��N*��ʱ��a2n+1-b=[��a+1��-1]2n+1-b=��a+1��2n+1++C2n+11��a+1��-1-b��
����b��[1��a]������b+1��[2��a+1]��
���ԣ����ҽ���b+1=a+1����b=aʱ��at-b�ܱ�a+1��������13�֣�
���ϣ�������[1��a]�ϴ���ʵ��b��ʹC=A��B��∅�������ҵ�b=1ʱ��C={y|y=a2n��n��N*}����b=aʱ��C={y|y=a2n+1��n��N}��
�����������ۺϿ��������е���͡��ȱ����еĶ��塢�����뼯���ۺϣ������˿�����������������������⡢��������������

��ϰ��ϵ�д�
�����Ŀ
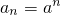 ��bn=��a+1��n+b��n=1��2��3����������a��2��a��N*��b��R��
��bn=��a+1��n+b��n=1��2��3����������a��2��a��N*��b��R��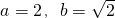 ʱ������{bn}�е�����������ܹ��ɵȱ����У�
ʱ������{bn}�е�����������ܹ��ɵȱ����У�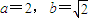 ʱ������{bn}�е�����������ܹ��ɵȱ����У�
ʱ������{bn}�е�����������ܹ��ɵȱ����У�