题目内容
在数列{an}和{bn}中,an=an,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.
(Ⅰ)若a1=b1,a2<b2,求数列{bn}的前n项和;
(Ⅱ)证明:当a=2,b=
时,数列{bn}中的任意三项都不能构成等比数列.
(Ⅰ)若a1=b1,a2<b2,求数列{bn}的前n项和;
(Ⅱ)证明:当a=2,b=
| 2 |
分析:(Ⅰ)根据a1=b1,可得b=-1,利用a2<b2,a≥2,可得a=2,从而可求数列{bn}的通项与前n项和;
(Ⅱ)设数列{bn}中的任意三项能构成等比数列,不妨设bx,by,bz(0≤x<y<z≤n)为任意三项成等比数列,所以by 2 =bx•bz,即3y2-3xz-(x+z-2
y)
=0,从而3y2-3xz=0,x+z-2
y=0,结合0≤x<y<z≤n,且x、y、z为整数,即可知当a=2,b=
时,数列{bn}中的任意三项都不能构成等比数列.
(Ⅱ)设数列{bn}中的任意三项能构成等比数列,不妨设bx,by,bz(0≤x<y<z≤n)为任意三项成等比数列,所以by 2 =bx•bz,即3y2-3xz-(x+z-2
| 2 |
| 2 |
| 2 |
| 2 |
解答:(Ⅰ)解:∵a1=b1,∴a=a+1+b,∴b=-1
∵a2<b2,∴a2<2a+1
∴1-
<a<1+
∵a≥2,∴a=2
∴bn=(a+1)n+b=3n-1
∴数列{bn}的前n项和为
=
n2+
;
(Ⅱ)证明:当a=2,b=
时,bn=(a+1)n+b=3n+
设数列{bn}中的任意三项能构成等比数列,不妨设bx,by,bz(0≤x<y<z≤n)为任意三项成等比数列,
则by 2 =bx•bz,即(3y+
)2=(3x+
)•(3z+
),化简得3y2-3xz-(x+z-2
y)
=0
∴3y2-3xz=0,x+z-2
y=0
∴x2-6xz+z2=0
∵0≤x<y<z≤n,且x、y、z为整数,
∴此方程无整数解.
故当a=2,b=
时,数列{bn}中的任意三项都不能构成等比数列.
∵a2<b2,∴a2<2a+1
∴1-
| 2 |
| 2 |
∵a≥2,∴a=2
∴bn=(a+1)n+b=3n-1
∴数列{bn}的前n项和为
| n(2+3n-1) |
| 2 |
| 3 |
| 2 |
| n |
| 2 |
(Ⅱ)证明:当a=2,b=
| 2 |
| 2 |
设数列{bn}中的任意三项能构成等比数列,不妨设bx,by,bz(0≤x<y<z≤n)为任意三项成等比数列,
则by 2 =bx•bz,即(3y+
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴3y2-3xz=0,x+z-2
| 2 |
∴x2-6xz+z2=0
∵0≤x<y<z≤n,且x、y、z为整数,
∴此方程无整数解.
故当a=2,b=
| 2 |
点评:本题考查了等差数列和等比数列的综合,考查数列求和,考查反证法思想.

练习册系列答案
相关题目
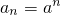 ,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.
,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.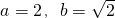 时,数列{bn}中的任意三项都不能构成等比数列.
时,数列{bn}中的任意三项都不能构成等比数列.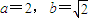 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;