题目内容
在数列{an}和{bn}中,an=an,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.设A={a1,a2,a3,…},B={b1,b2,b3,…},试问在区间[1,a]上是否存在实数b使得C=A∩B≠∅.若存在,求出b的一切可能的取值及相应的集合C;若不存在,试说明理由.
分析:设存在实数b∈[1,a],使C=A∩B≠∅,设m0∈C,则m0∈A,且m0∈B,利用数列的通项,可得at=(a+1)s+b,从而可得s=
,根据a,t,s∈N*,且a≥2,可得at-b能被a+1整除,再分类讨论,即可求得结论.
| at-b |
| a+1 |
解答:解:设存在实数b∈[1,a],使C=A∩B≠∅,
设m0∈C,则m0∈A,且m0∈B,
设m0=at(t∈N*),m0=(a+1)s+b(s∈N*),则at=(a+1)s+b,所以s=
,
因为a,t,s∈N*,且a≥2,所以at-b能被a+1整除. …(4分)
(1)当t=1时,因为b∈[1,a],a-b∈[0,a-1],所以s=
∉N*; …(5分)
(2)当t=2n(n∈N*)时,a2n-b=[(a+1)-1]2n-b=(a+1)2n+…-
(a+1)+1-b,
由于b∈[1,a],所以b-1∈[0,a-1],0≤b-1<a+1,
所以,当且仅当b=1时,at-b能被a+1整除.…(7分)
(3)当t=2n+1(n∈N*)时,a2n+1-b=[(a+1)-1]2n+1-b=(a+1)2n+1+…+
(a+1)-1-b,
由于b∈[1,a],所以b+1∈[2,a+1],
所以,当且仅当b+1=a+1,即b=a时,at-b能被a+1整除..…(9分)
综上,在区间[1,a]上存在实数b,使C=A∩B≠∅成立,
当b=1时,C={y|y=a2n,n∈N*};
当b=a时,C={y|y=a2n+1,n∈N*}. …(10分)
设m0∈C,则m0∈A,且m0∈B,
设m0=at(t∈N*),m0=(a+1)s+b(s∈N*),则at=(a+1)s+b,所以s=
| at-b |
| a+1 |
因为a,t,s∈N*,且a≥2,所以at-b能被a+1整除. …(4分)
(1)当t=1时,因为b∈[1,a],a-b∈[0,a-1],所以s=
| a-b |
| a+1 |
(2)当t=2n(n∈N*)时,a2n-b=[(a+1)-1]2n-b=(a+1)2n+…-
| C | 1 2n |
由于b∈[1,a],所以b-1∈[0,a-1],0≤b-1<a+1,
所以,当且仅当b=1时,at-b能被a+1整除.…(7分)
(3)当t=2n+1(n∈N*)时,a2n+1-b=[(a+1)-1]2n+1-b=(a+1)2n+1+…+
| C | 1 2n+1 |
由于b∈[1,a],所以b+1∈[2,a+1],
所以,当且仅当b+1=a+1,即b=a时,at-b能被a+1整除..…(9分)
综上,在区间[1,a]上存在实数b,使C=A∩B≠∅成立,
当b=1时,C={y|y=a2n,n∈N*};
当b=a时,C={y|y=a2n+1,n∈N*}. …(10分)
点评:本题考查演绎推理,考查数列知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
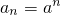 ,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.
,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.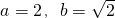 时,数列{bn}中的任意三项都不能构成等比数列.
时,数列{bn}中的任意三项都不能构成等比数列.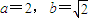 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;