题目内容
在数列{an}和{bn}中,an=an,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.(Ⅰ)若a1=b1,a2<b2,求数列{bn}的前n项和;
(Ⅱ)证明:当a=2,b=
| 2 |
(Ⅲ)设A={a1,a2,a3,…},B={b1,b2,b3,…},试问在区间[1,a]上是否存在实数b使得C=A∩B≠∅.若存在,求出b的一切可能的取值及相应的集合C;若不存在,试说明理由.
分析:(I)由a1=b1,a2<b2,结合已知可建立a,b的方程,从而可求a,b,进一步求出数列bn的通项及前n项和
(II)a=2, b=
结合(I)知bn=3n+
,假设amanat(m.n.t∈N+)成等比数列,且m≠n≠t,由假设推导可得3n2-3mt=
(m+t-2n),结合m≠t≠n∈N+的条件可知矛盾.
(III)设存在实数b∈[1,a],使C=A∩B≠∅,若m0∈C,则m0∈A,且m0∈B,
由m0∈A可设m0=at,由m0∈B可设mo=(a+1)s+b,整理可得s=
分t为奇偶情况分别进行讨论,若推出矛盾,则说明不存在,否则存在符合条件的实数b
(II)a=2, b=
| 2 |
| 2 |
| 2 |
(III)设存在实数b∈[1,a],使C=A∩B≠∅,若m0∈C,则m0∈A,且m0∈B,
由m0∈A可设m0=at,由m0∈B可设mo=(a+1)s+b,整理可得s=
| at-b |
| a+1 |
解答:解:(Ⅰ)因为a1=b1,所以a=a+1+b,b=-1,(1分)
由a2<b2,得a2-2a-1<0,
所以1-
<a<1+
,(3分)
因为a≥2且a∈N*,所以a=2,(4分)
所以bn=3n-1,{bn}是等差数列,
所以数列{bn}的前n项和Sn=
(b1+bn)=
n2+
n.(5分)
(Ⅱ)由已知bn=3n+
,假设3m+
,3n+
,3t+
成等比数列,其中m,n,t∈N*,且彼此不等,
则(3n+
)2=(3m+
)(3t+
),(6分)
所以9n2+6
n+2=9mt+3
m+3
t+2,
所以3n2-3mt=(m+t-2n)
,
若m+t-2n=0,则3n2-3mt=0,可得m=t,与m≠t矛盾;(7分)
若m+t-2n≠0,则m+t-2n为非零整数,(m+t-2n)
为无理数,
所以3n2-3mt为无理数,与3n2-3mt是整数矛盾.(9分)
所以数列{bn}中的任意三项都不能构成等比数列.
(Ⅲ)设存在实数b∈[1,a],使C=A∩B≠∅,
设m0∈C,则m0∈A,且m0∈B,
设m0=at(t∈N*),m0=(a+1)s+b(s∈N*),
则at=(a+1)s+b,所以s=
,
因为a,t,s∈N*,且a≥2,所以at-b能被a+1整除.(10分)
(1)当t=1时,因为b∈[1,a],a-b∈[0,a-1],
所以s=
∉N*;(11分)
(2)当t=2n(n∈N*)时,a2n-b=[(a+1)-1]2n-b=(a+1)2n+-C2n1(a+1)+1-b,
由于b∈[1,a],所以b-1∈[0,a-1],0≤b-1<a+1,
所以,当且仅当b=1时,at-b能被a+1整除.(12分)
(3)当t=2n+1(n∈N*)时,a2n+1-b=[(a+1)-1]2n+1-b=(a+1)2n+1++C2n+11(a+1)-1-b,
由于b∈[1,a],所以b+1∈[2,a+1],
所以,当且仅当b+1=a+1,即b=a时,at-b能被a+1整除.(13分)
综上,在区间[1,a]上存在实数b,使C=A∩B≠∅成立,且当b=1时,C={y|y=a2n,n∈N*};当b=a时,C={y|y=a2n+1,n∈N}.
由a2<b2,得a2-2a-1<0,
所以1-
| 2 |
| 2 |
因为a≥2且a∈N*,所以a=2,(4分)
所以bn=3n-1,{bn}是等差数列,
所以数列{bn}的前n项和Sn=
| n |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由已知bn=3n+
| 2 |
| 2 |
| 2 |
| 2 |
则(3n+
| 2 |
| 2 |
| 2 |
所以9n2+6
| 2 |
| 2 |
| 2 |
所以3n2-3mt=(m+t-2n)
| 2 |
若m+t-2n=0,则3n2-3mt=0,可得m=t,与m≠t矛盾;(7分)
若m+t-2n≠0,则m+t-2n为非零整数,(m+t-2n)
| 2 |
所以3n2-3mt为无理数,与3n2-3mt是整数矛盾.(9分)
所以数列{bn}中的任意三项都不能构成等比数列.
(Ⅲ)设存在实数b∈[1,a],使C=A∩B≠∅,
设m0∈C,则m0∈A,且m0∈B,
设m0=at(t∈N*),m0=(a+1)s+b(s∈N*),
则at=(a+1)s+b,所以s=
| at-b |
| a+1 |
因为a,t,s∈N*,且a≥2,所以at-b能被a+1整除.(10分)
(1)当t=1时,因为b∈[1,a],a-b∈[0,a-1],
所以s=
| a-b |
| a+1 |
(2)当t=2n(n∈N*)时,a2n-b=[(a+1)-1]2n-b=(a+1)2n+-C2n1(a+1)+1-b,
由于b∈[1,a],所以b-1∈[0,a-1],0≤b-1<a+1,
所以,当且仅当b=1时,at-b能被a+1整除.(12分)
(3)当t=2n+1(n∈N*)时,a2n+1-b=[(a+1)-1]2n+1-b=(a+1)2n+1++C2n+11(a+1)-1-b,
由于b∈[1,a],所以b+1∈[2,a+1],
所以,当且仅当b+1=a+1,即b=a时,at-b能被a+1整除.(13分)
综上,在区间[1,a]上存在实数b,使C=A∩B≠∅成立,且当b=1时,C={y|y=a2n,n∈N*};当b=a时,C={y|y=a2n+1,n∈N}.
点评:本题综合考查了数列的求和、等比数列的定义、数列与集合综合,考查了考生的逻辑推理能力与分析问题、解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
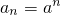 ,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.
,bn=(a+1)n+b,n=1,2,3,…,其中a≥2且a∈N*,b∈R.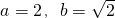 时,数列{bn}中的任意三项都不能构成等比数列.
时,数列{bn}中的任意三项都不能构成等比数列.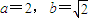 时,数列{bn}中的任意三项都不能构成等比数列;
时,数列{bn}中的任意三项都不能构成等比数列;