题目内容
15．方程（x-2）2+（y+1）2=1表示的曲线关于点T（-3，2）的对称曲线方程是（ ）| A． | （x+8）2+（y-5）2=1 | B． | （x-7）2+（y+4）2=2 | C． | （x+3）2+（y-2）2=1 | D． | （x+4）2+（y+3）2=2 |
分析 求出圆的圆心坐标，然后求解对称圆的圆心坐标，即可求出圆的方程．
解答 解：圆（x-2）2+（y+1）2=1的圆心坐标（2，-1），半径为1．
圆心（2，-1）关于P（-3，2）对称的点的坐标为（a，b），
则a+2=-6，b-1=4，解得a=-8，b=5，所求对称圆的圆心坐标（-8，5），半径为1．
∴圆（x-2）2+（y+1）2=1表示的曲线关于点T（-3，2）的对称曲线方程是：（x+8）2+（y-5）2=1．
故选：A．
点评 本题考查对称圆的方程的求法，注意求解圆的方程，就是求解圆的圆心与半径，注意对称知识的应用．
练习册系列答案
相关题目
20．已知集合U={x|x＞0}，∁UA={x|0＜x＜2}，则集合A=（ ）
| A． | {x|x≤0或x≥2} | B． | {x|x＜0或x＞2} | C． | {x|x≥2} | D． | {x|x＞2} |
4．已知函数f（x）=asin（πx+α）+bcos（πx+β），且f（2014）=3，则f（2015）的值是（ ）
| A． | -1 | B． | -2 | C． | -3 | D． | 1 |
13．
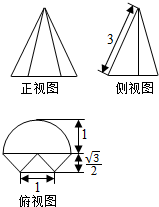一个几何体的三视图如图所示，其俯视图为一个半圆和一个等腰梯形，则该几何体的体积为（ ）
一个几何体的三视图如图所示，其俯视图为一个半圆和一个等腰梯形，则该几何体的体积为（ ）| A． | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | B． | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ | C． | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | D． | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ |