题目内容
（2010•桂林二模）（注意：在试题卷上作答无效）桂林某学校从参加高三年级第二次模拟考试的学生中随机抽出100名学生，将其数学成绩（均为整数）分成五段[50，70），[70，90），[90，110），[110，130），[130，150]后得到如右部分频率分布直方图，分析图形的信息，回答下列问题：
（Ⅰ）求分数在[90，110）内的频率和学生数，并补全这个频率分布直方图；
（Ⅱ）现从分数段[90，150]的学生中随机抽取2人给予助学金奖励，抽到的学生成绩在[90，110）内每人奖励100元，在[100，130）内每人奖励200元，在[130，150）内每人奖励300元，用ξ表示抽取结束后总的奖励金额，求ξ的分布列和数学期望．
分析：（I）根据所求的频率的和为1可求出分数在[90，110）内的频率，该频率乘以样本容量，可求频数，即为分数在[90，110）内的学生数，然后计算出在[90，110）的高，补全图形即可；
（II）先分别求出成绩在[90，110）、[110，130）、[130，150）内的人数，ξ的可能取值为200，300，400，500，600，然后根据古典概型的概率公式求出相应的概率，列出分布列，最后根据数学期望公式解之即可．
（II）先分别求出成绩在[90，110）、[110，130）、[130，150）内的人数，ξ的可能取值为200，300，400，500，600，然后根据古典概型的概率公式求出相应的概率，列出分布列，最后根据数学期望公式解之即可．
解答：解：（I）设分数在[90，110）内的频率为x，根据频率分布直方图有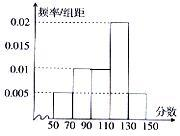
∵1-（0.005+0.01+0.02+0.005）×20=0.2
∴x=0.2，100×0.2=20人，
=0.01
∴分数在[90，110）内的频率为0.2，学生数为20人
所以频率分布直方图如右图所示．
（II）由图知成绩在[90，110）内有100×0.01×20=20人，在[110，130）内有100×0.02×20=40人，
在[130，150）内有100×0.005×20=10人，共有70人
ξ的可能取值为200，300，400，500，600
则P（ξ=200）=
=
，P（ξ=300）=
=
P（ξ=400）=
=
P（ξ=500）=
=
P（ξ=600）=
=
∴ξ的分布列为
∴Eξ=200×
+300×
+400×
+500×
+600×
=360
答：所求的数学期望为360元．
∵1-（0.005+0.01+0.02+0.005）×20=0.2
∴x=0.2，100×0.2=20人，
| 0.2 |
| 20 |
∴分数在[90，110）内的频率为0.2，学生数为20人
所以频率分布直方图如右图所示．
（II）由图知成绩在[90，110）内有100×0.01×20=20人，在[110，130）内有100×0.02×20=40人，
在[130，150）内有100×0.005×20=10人，共有70人
ξ的可能取值为200，300，400，500，600
则P（ξ=200）=
| ||
|
| 38 |
| 483 |
| ||||
|
| 160 |
| 483 |
P（ξ=400）=
| ||||||
|
| 196 |
| 483 |
P（ξ=500）=
| ||||
|
| 80 |
| 483 |
P（ξ=600）=
| ||
|
| 9 |
| 483 |
∴ξ的分布列为
| ξ | 200 | 300 | 400 | 500 | 600 | ||||||||||
| P |
|
|
|
|
|
| 38 |
| 483 |
| 160 |
| 483 |
| 196 |
| 483 |
| 80 |
| 483 |
| 9 |
| 483 |
答：所求的数学期望为360元．
点评：本题主要考查了频率分布直方图，以及离散型随机变量的分布列和数学期望，同时考查了计算能力，属于中档题．
练习册系列答案
相关题目