题目内容
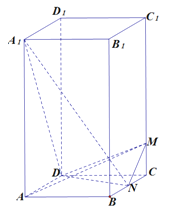
【题目】如图,在正四棱柱![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,设二面角
上,设二面角![]() 的大小为
的大小为![]() .
.
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)建立空间直角坐标系,求出![]() 坐标,设M(0,1,z),分别求出面A1DN和平面MDN的法向量坐标,再由已知可得
坐标,设M(0,1,z),分别求出面A1DN和平面MDN的法向量坐标,再由已知可得![]() 坐标,即可求解;
坐标,即可求解;
(2)根据(1)的法向量坐标,运用空间向量面面角公式,即可得出结论.
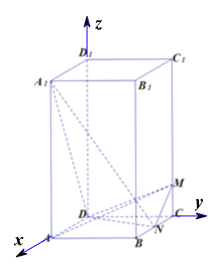
以D为原点,DA为x轴正半轴,DC为y轴正半轴,DD1为z轴正半轴,
建立空间直角坐标系,则A(1,0,0),A1(1,0,2),
N(![]() ,1,0),C(0,1,0)),设M(0,1,z),
,1,0),C(0,1,0)),设M(0,1,z),
设平面MDN的法向量![]() ,
,
![]()
则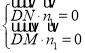 ,即
,即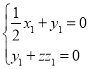 ,
,
取![]() ,则
,则![]() ,
,
平面MDN的法向量的一个法向量为![]()
设平面A1DN的法向量为![]() ,则
,则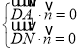 ,
,
即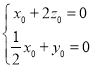 ,取
,取![]() ,则
,则![]() ,
,![]() ,
,
则![]() .
.
(1)由题意:![]()
![]() ,
,
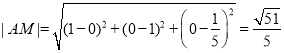 ;
;
(2)由题意: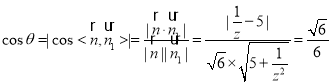
解得![]() .
.

练习册系列答案
相关题目