题目内容
在棱长为1的正方体AC1中,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PA⊥BD1,则动点P的轨迹的长度为
.
| 2 |
| 2 |
分析:画出图形,由线面垂直的判定得到BD1⊥面AB1C,从而得到动点P的轨迹为线段B1C,则长度可求.
解答: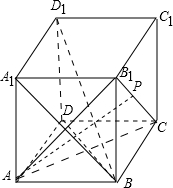 解:如图,
解:如图,
连结AC,BD,则AC⊥BD,
∵D1D⊥面ABCD,∴D1D⊥AC,
又D1D∩DB=D,∴AC⊥面D1DB,∴BD1⊥AC.
连结A1B,AB1,则A1B⊥AB1,
∵A1D1⊥面A1ABB1,∴A1D1⊥AB1.
又A1D1∩A1B=A1,∴AB1⊥面A1BD1,∴BD1⊥AB1.
又AB1∩AC=A,∴BD1⊥面AB1C,∴P点的轨迹为线段B1C.
∴动点P的轨迹的长度为|B1C|=
.
故答案为:
.
 解:如图,
解:如图,连结AC,BD,则AC⊥BD,
∵D1D⊥面ABCD,∴D1D⊥AC,
又D1D∩DB=D,∴AC⊥面D1DB,∴BD1⊥AC.
连结A1B,AB1,则A1B⊥AB1,
∵A1D1⊥面A1ABB1,∴A1D1⊥AB1.
又A1D1∩A1B=A1,∴AB1⊥面A1BD1,∴BD1⊥AB1.
又AB1∩AC=A,∴BD1⊥面AB1C,∴P点的轨迹为线段B1C.
∴动点P的轨迹的长度为|B1C|=
| 2 |
故答案为:
| 2 |
点评:本题考查了轨迹方程,考查了直线和平面垂直的判定即性质,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 在线段AD1上运动,给出以下四个命题:
在线段AD1上运动,给出以下四个命题: 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1 和BB1的中点,那么直线AM与CN所成角的余弦值是( )
在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1 和BB1的中点,那么直线AM与CN所成角的余弦值是( ) (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.
(2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.