题目内容
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 两点(
两点(![]() 在第一象限),以
在第一象限),以![]() 为直径的圆分别与
为直径的圆分别与![]() 轴相切于
轴相切于![]() 两点,则下列结论正确的是( )
两点,则下列结论正确的是( )
A.抛物线![]() 的焦点
的焦点![]() 坐标为
坐标为![]() B.
B.![]()
C.![]() 为抛物线
为抛物线![]() 上的动点,
上的动点,![]() ,则
,则![]() D.
D.![]()
【答案】ABD
【解析】
A,由抛物线方程可得焦点坐标;B,由题意可得直线PQ的方程与抛物线联立求出P,Q的坐标,进而可得PQ的长度;C,由抛物线的性质到焦点的距离等于到准线的距离距离可得|MF|+|MN|的最小值;D,由题意可得A,B的坐标,进而求出AB的值;然后判断所给命题的真假.
A,由题意可得抛物线的焦点F(2,0),所以A正确;
B,由题意设直线PQ的方程为:y![]() (x﹣2),
(x﹣2),
与抛物线联立整理可得:3x2﹣20x+12=0,解得:x![]() 或6,
或6,
代入直线PQ方程可得y分别为:![]() ,4
,4![]() ,
,
由题意可得P(6,4![]() ),Q(
),Q(![]() ,
,![]() );
);
所以|PQ|=6![]() 4
4![]() ,所以B正确;
,所以B正确;
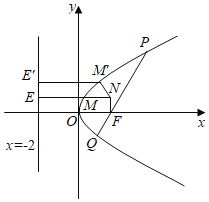
C,如图M在抛物线上,ME垂直于准线交于E,可得|MF|=ME|,
所以|MF|+|MN|=|ME|+|MN|≥NE=2+2=4,当N,M,E三点共线时,|MF|+|MN|最小,且最小值为4,所以C不正确;
D,因为P(6,4![]() ),Q(
),Q(![]() ,
,![]() ),所以PF,QF的中点分别为:(3,2
),所以PF,QF的中点分别为:(3,2![]() ),(
),(![]() ,
,![]() ),
),
所以由题意可得A(0,2![]() ),B(0,
),B(0,![]() ),
),
所以|AB|=2![]() ,所以D正确;
,所以D正确;
故选:ABD.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
的人群中按分层抽样抽取7人,再从中选2人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
(3)小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
【题目】在第十五次全国国民阅读调查中,某地区调查组获得一个容量为![]() 的样本,其中城镇居民
的样本,其中城镇居民![]() 人,农村居民
人,农村居民![]() 人.在这些居民中,经常阅读的城镇居民
人.在这些居民中,经常阅读的城镇居民![]() 人,农村居民
人,农村居民![]() 人.
人.
(Ⅰ)填写下面列联表,并判断是否有![]() 的把握认为,经常阅读与居民居住地有关?
的把握认为,经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 |
|
| |
不经常阅读 | |||
合计 |
|
(Ⅱ)从该地区居民城镇的居民中,随机抽取![]() 位居民参加一次阅读交流活动,记这
位居民参加一次阅读交流活动,记这![]() 位居民中经常阅读的人数为
位居民中经常阅读的人数为![]() ,若用样本的频率作为概率,求随机变量
,若用样本的频率作为概率,求随机变量![]() 的分布列和期望.
的分布列和期望.
附: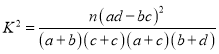 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
