题目内容
如图，E、F分别为正方形的面ADD1A1与面BCC1B1的中心，则四边形BFD1E在正方体的面上的正投影影可能是（要求：把可能的图的序号都填上）
考点：平行投影及平行投影作图法
专题：计算题,空间位置关系与距离
分析：按照三视图的作法：上下、左右、前后三个方向的射影，四边形的四个顶点在三个投影面上的射影，再将其连接即可得到三个视图的形状，按此规则对题设中所给的四图形进行判断即可．
解答：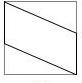
解：因为正方体是对称的几何体，
所以四边形BFD1E在该正方体的面上的射影可分为：自上而下、自左至右、由前及后三个方向的射影，
也就是在面ABCD、面ABB1A1、面ADD1A1上的射影．
四边形BFD1E在面ABCD和面ABB1A1上的射影相同，如图②所示；
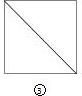
四边形BFD1E在该正方体对角面的ABC1D1内，它在面ADD1A1上的射影显然是一条线段，如图③所示．
故②③正确
故答案为：②③．
解：因为正方体是对称的几何体，所以四边形BFD1E在该正方体的面上的射影可分为：自上而下、自左至右、由前及后三个方向的射影，
也就是在面ABCD、面ABB1A1、面ADD1A1上的射影．
四边形BFD1E在面ABCD和面ABB1A1上的射影相同，如图②所示；
四边形BFD1E在该正方体对角面的ABC1D1内，它在面ADD1A1上的射影显然是一条线段，如图③所示．
故②③正确
故答案为：②③．
点评：本题考查简单空间图形的三视图，考查根据作三视图的规则来作出三个视图的能力，三视图是高考的新增考点，不时出现在高考试题中，应予以重视．
练习册系列答案
相关题目
用二分法求方程lgx=3-x的近似解，可以取的一个区间是（ ）
| A、（0，1） | B、（1，2） | C、（2，3） | D、（3，4） |
若一个圆柱的正视图与其侧面展开图相似，则这个圆柱的侧面积与全面积之比为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知棱锥的正视图与俯视图如图所示，俯视图是边长为2的正三角形，该三棱锥的侧视图可能为（ ）
如图，AB是⊙O的直径，VA垂直⊙O所在的平面，点C是圆周上不同于A，B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是（ ）| A、MN∥AB | B、MN与BC所成的角为45° | C、OC⊥平面VAC | D、平面VAC⊥平面VBC |
过抛物线x2=4y的焦点作直线l交抛物线于A，B两点，分别过A，B作抛物线的切线l1，l2，则l1与l2的交点P的轨迹方程是（ ）
| A、y=-1 | B、y=-2 | C、y=x-1 | D、y=-x-1 |
阅读程序框图，若输入m=4，则输出S等于（ ）
| A、8 | B、12 | C、20 | D、30 |