题目内容
【题目】设f(x)是定义在区间(1,+∞)上的函数,其导函数为![]() .如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得
.如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得![]() =h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
=h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
(1)设函数![]() ,其中b为实数.
,其中b为实数.
①求证:函数f(x)具有性质P(a).②求函数f(x)的单调区间.
(2)已知函数g(x)具有性质P(2),给定x1,x2∈(1,+∞),x1<x2.设m为实数, ![]() ,且
,且![]() .若
.若![]() ,求实数m的取值范围
,求实数m的取值范围
【答案】(1)当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为(1,![]() ),单调增区间为(
),单调增区间为(![]() ,+∞).
,+∞).
(2)(0,1)
【解析】
解:(1)由f(x)=ln x+![]() ,得f′(x)=
,得f′(x)=![]() .
.
①证明:因为x>1时,h(x)=![]() >0,所以函数f(x)具有性质P(b).
>0,所以函数f(x)具有性质P(b).
②当b≤2时,由x>1得x2-bx+1≥x2-2x+1=(x-1)2>0,
所以f′(x)>0.从而函数f(x)在区间(1,+∞)上单调递增.
当b>2时,令x2-bx+1=0得
x1=![]() ,x2=
,x2=![]() .
.
因为x1=![]() =
=![]() <
<![]() <1,
<1,
x2=![]() >1,
>1,
所以当x∈(1,x2)时,f′(x)<0;当x∈(x2,+∞)时,f′(x)>0;当x=x2时,f′(x)=0.从而函数f(x)在区间(1,x2)上单调递减,在区间(x2,+∞)上单调递增.
综上所述,当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为(1,![]() ),单调增区间为(
),单调增区间为(![]() ,+∞).
,+∞).
(2)由题设知,g(x)的导函数
g′(x)=h(x)(x2-2x+1),
其中函数h(x)>0对于任意的x∈(1,+∞)都成立,
所以当x>1时,g′(x)=h(x)(x-1)2>0,
从而g(x)在区间(1,+∞)上单调递增.
①当m∈(0,1)时,
有α=mx1+(1-m)x2>mx1+(1-m)x1=x1,
α<mx2+(1-m)x2=x2,即α∈(x1,x2),
同理可得β∈(x1,x2).
所以由g(x)的单调性知g(α),g(β)∈(g(x1),g(x2)),从而有|g(α)-g(β)|<|g(x1)-g(x2)|,符合题意.
②当m≤0时,α=mx1+(1-m)x2≥mx2+(1-m)x2=x2,β=(1-m)x1+mx2≤(1-m)x1+mx1=x1,于是由α>1,β>1及g(x)的单调性知g(β)≤g(x1)<g(x2)≤g(α),
所以|g(α)-g(β)|≥|g(x1)-g(x2)|,与题意不符.
③当m≥1时,同理可得α≤x1,β≥x2,
进而得|g(α)-g(β)|≥|g(x1)-g(x2)|,与题意不符.
综上所述,所求的m的取值范围为(0,1).

【题目】中国人民大学发布的《中国大学生创业报告》显示,在国家“双创”政策的引导下,随着社会各方对于大学生创业实践的支持力度不断加强,大学生创业意向高涨,近九成的在校大学生曾考虑过创业,近两成的学生有强烈的创业意向. 数据充分表明,大学生正以饱满的热情投身到创新创业的大潮之中,大学生创业实践正呈现出生机勃勃的态势。小张大学毕业后从2008年年初开始创业,下表是2019年春节他将自己从2008—2018年的净利润按年度给出的一个总的统计表(为方便运算,数据作了适当的处理,单位:万元).
年度 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
利润 | 6 | 7 | 8 | 9 | 10 | 10 | 11 | 12 | 13 | 13 | 14 |
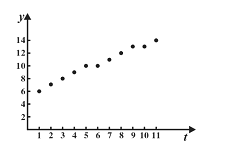
(Ⅰ)散点图如图所示,根据散点图指出年利润![]() (单位:万元)和年份序号
(单位:万元)和年份序号![]() 之间是否具有线性关系?并用相关系数说明用线性回归模型描述年净利润
之间是否具有线性关系?并用相关系数说明用线性回归模型描述年净利润![]() 与年份序号
与年份序号![]() 之间关系的效果;
之间关系的效果;
(Ⅱ)试用线性回归模型描述年净利润![]() 与年份序号
与年份序号![]() 之间的关系:求出年净利润
之间的关系:求出年净利润![]() 关于年份序号
关于年份序号![]() 的回归方程(系数精确到0.1),并帮小张估计他2019年可能赚到的净利润.
的回归方程(系数精确到0.1),并帮小张估计他2019年可能赚到的净利润.
附注:参考数据![]() .
.
参考公式: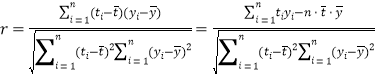 .
.![]() 且
且![]() 越大拟合效果越好.回归方程
越大拟合效果越好.回归方程![]() 斜率的最小二乘法估计公式为:
斜率的最小二乘法估计公式为: .
.
【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: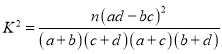 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】随着5G商用进程的不断加快,手机厂商之间围绕5G用户的争夺越来越激烈,5G手机也频频降低身价飞人寻常百姓家.某科技公司为了给自己新推出的5G手机定价,随机抽取了100人进行调查,对其在下一次更换5G手机时,能接受的价格(单位:元)进行了统计,得到结果如下表,已知这100个人能接受的价格都在![]() 之间,并且能接受的价格的平均值为2350元(同一组的数据用该组区间的中点值代替).
之间,并且能接受的价格的平均值为2350元(同一组的数据用该组区间的中点值代替).
分组 | 一 | 二 | 三 | 四 | 五 |
手机价格X(元) |
|
|
|
|
|
频数 | 10 | x | y | 20 | 20 |
(1)现用分层抽样的方法从第一、二、三组中随机抽取6人,将该样本看成一个总体,从中随机抽取2人,求其中恰有1人能接受的价格不低于2000元的概率;
(2)若人们对5G手机能接受的价格X近似服从正态分布![]() ,其中
,其中![]() 为样本平均数
为样本平均数![]() ,
,![]() 为样本方差
为样本方差![]() ,求
,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
