题目内容
对数列 ,规定
,规定 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中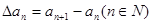 , 对自然数
, 对自然数 ,规定
,规定 为
为 的
的 阶差分数列,其中
阶差分数列,其中 .
.
(1)已知数列 的通项公式
的通项公式 ,试判断
,试判断 ,
, 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列 首项
首项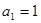 ,且满足
,且满足 ,求数列
,求数列 的通项公式。
的通项公式。
(3)对(2)中数列 ,是否存在等差数列
,是否存在等差数列 ,使得
,使得 对一切自然
对一切自然 都成立?若存在,求数列
都成立?若存在,求数列 的通项公式;若不存在,则请说明理由。
的通项公式;若不存在,则请说明理由。
【答案】
(1)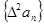 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
(2) ,
, ,
, ,
, ,猜想:
,猜想: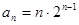
证明:数学归纳法。
(3)组合数性质证得,存在等差数列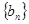 ,
, ,使得
,使得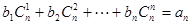 对一切自然
对一切自然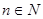 都成 。
都成 。
【解析】
试题分析:(1)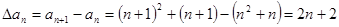 , 1分
, 1分
∴ 是首项为4,公差为2的等差数列。
2分
是首项为4,公差为2的等差数列。
2分
 3分
3分
∴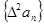 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
4分
(2)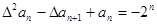 ,即
,即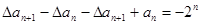 ,即
,即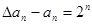 ,∴
,∴ 6分
6分
∵ ,∴
,∴ ,
, ,
, ,猜想:
,猜想: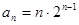
7分
证明:ⅰ)当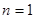 时,
时,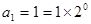 ;
;
ⅱ)假设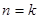 时,
时, 8分
8分
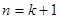 时,
时, 结论也成立
结论也成立
∴由ⅰ)、ⅱ)可知,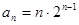 10分
10分
(3)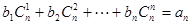 ,即
,即 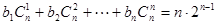
. ...11分
∵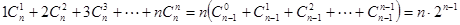 13分
13分
∴存在等差数列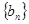 ,
, ,使得
,使得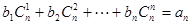 对一切自然
对一切自然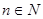 都成 14分
都成 14分
考点:等差数列、等比数列的基础知识,数学归纳法,组合数的性质。
点评:中档题,本题综合性较强,将数列、数学归纳法、二项式系数的性质、组合数公式等综合考查。利用“功能、猜想、证明”的方法,研究得到数列的特征,是常见题型。(3)小题利用二项式系数的性质及组合数公式,得到证明恒等式的目的。

练习册系列答案
相关题目
 ,规定
,规定 为数列
为数列 N*).对正整数k,规定
N*).对正整数k,规定 为
为 .
. ,且满足
,且满足 ,求数列
,求数列 是等差数列,使得
是等差数列,使得 对一切正整数
对一切正整数 N*都成立,求
N*都成立,求 ;
; 设
设 若
若 成立,求最小正整数
成立,求最小正整数 的值.
的值. ,规定
,规定 为数列
为数列 .对自然数
.对自然数 ,规定
,规定 为数列
为数列

 ,则
,则 ;
; ,且满足
,且满足 ,则数列
,则数列 ,规定
,规定 为数列
为数列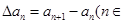 N*).对正整数k,规定
N*).对正整数k,规定  为
为 .
. ,且满足
,且满足 ,求数列
,求数列 是等差数列,使得
是等差数列,使得 对一切正整数
对一切正整数 N*都成立,求
N*都成立,求 ;
; 设
设 若
若 成立,求最小正整数
成立,求最小正整数 的值.
的值.