题目内容
本小题共13分)
对数列 ,规定
,规定 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中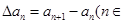 N*).对正整数k,规定
N*).对正整数k,规定  为
为 的k阶差分数列,其中
的k阶差分数列,其中
 .
.
(Ⅰ)若数列 的首项
的首项 ,且满足
,且满足 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)对(Ⅰ)中的数列 ,若数列
,若数列 是等差数列,使得
是等差数列,使得
 对一切正整数
对一切正整数 N*都成立,求
N*都成立,求 ;
;
(Ⅲ) 在(Ⅱ)的条件下,令 设
设 若
若 成立,求最小正整数
成立,求最小正整数 的值.
的值.
【答案】
解:(Ⅰ)由 及
及 ,
,
得  ,
,
∴
∴ ———————————————2分
———————————————2分
∴数列 是首项为
是首项为 公差为
公差为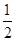 的等差数列,
的等差数列,
∴
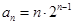 .————————4分
.————————4分
(Ⅱ)∵  ,
,
∴ 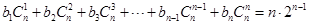 .
.
∵ ,
,

∴  .————————————9分
.————————————9分
(Ⅲ)由(Ⅱ)得  , ①
, ①
有
 , ②
, ②
①-② 得  ,
,
∴ , ——————————10分
, ——————————10分
又 ,
,
∴ ,
,
∴ 是递增数列,且
是递增数列,且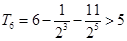 ,
,
∴ 满足条件的最小正整数 的值为6.————————13分
的值为6.————————13分
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 .
. 满足
满足 (
( ),且
),且 ,
, .
. ,数列
,数列 的前
的前 ,求使不等式
,求使不等式 对一切
对一切 的值;
的值; 是否存在
是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 分别判断2个选项是错误的,还有两道题因不理解题意只好乱猜.
分别判断2个选项是错误的,还有两道题因不理解题意只好乱猜. ,设函数
,设函数 .
. 在
在 上的单调递增区间;
上的单调递增区间; 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, ,
, ,
, ,求边
,求边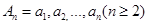 满足
满足 ,数列
,数列 为
为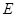 数列,记
数列,记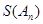 =
= .
.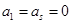 ,且
,且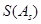 〉0的
〉0的 ,n=2000,证明:E数列
,n=2000,证明:E数列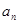 =2011;
=2011;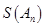 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列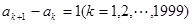 .所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000
.所以A5是首项为12,公差为1的等差数列.所以a2000=12+(2000—1)×1=2011.充分性,由于a2000—a1000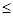 1,a2000—a1000
1,a2000—a1000 是递增数列.综上,结论得证。
是递增数列.综上,结论得证。