题目内容
空间四边形ABCD中，AD=BC=2,E,F分别是AB,CD的中点，EF＝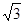 
，则异面直线AD,BC所成的角为( )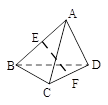
| A．30° | B．60° | C．90° | D．120° |
B
解析试题分析：设G为AC的中点，由已知中AD=BC=2，E、F分别是AB、CD的中点，若EF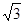＝，根据三角形中位线定理，我们易求出∠EGF为异面直线AD、BC所成的角（或其补角），解三角形EGF即可得到答案.
考点：异面直线所成的角.
练习册系列答案
相关题目
已知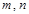
为两条不同直线,
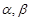为两个不同平面,给出下列命题:
①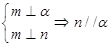
②
③
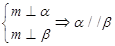④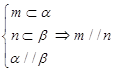
其中的正确命题序号（ ）
| A．③④ | B．②③ |
| C．①② | D．①②③④ |
把正方形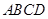
沿对角线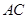
折起,当以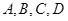
四点为顶点的三棱锥体积最大时，直线
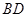和平面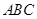
所成的角的大小为（ ）
A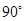． | B． | C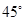． | D． |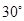
平行六面体ABCD
A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )
| A．3 | B．4 | C．5 | D．6 |
设l是直线，α，β是两个不同的平面，下列为真命题的是( )
| A．若l∥α，l∥β，则α∥β | B．若l∥α，l⊥β，则α⊥β |
| C．若α⊥β，l⊥α，则l⊥β | D．若α⊥β，l∥α，则l⊥β |
设m，n是两条不同的直线，α，β是两个不同的平面．则下列结论中正确的是( )
| A．若m∥α，n∥α，则m∥n |
| B．若m∥α，m∥β，则α∥β |
| C．若m∥n，m⊥α，则n⊥α |
| D．若m∥α，α⊥β，则m⊥β |
如图所示，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ADB沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD.则在三棱锥A－BCD中，下列命题正确的是( )．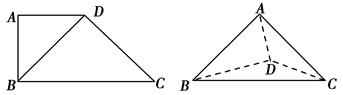
| A．平面ABD⊥平面ABC |
| B．平面ADC⊥平面BDC |
| C．平面ABC⊥平面BDC |
| D．平面ADC⊥平面ABC |
已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l?α，l?β，则( )．
| A．α∥β且l∥α |
| B．α⊥β且l⊥β |
| C．α与β相交，且交线垂直于l |
| D．α与β相交，且交线平行于l |