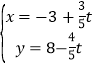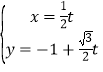题目内容
【题目】在四棱锥S-ABCD中，底面ABCD为长方形，
底面
，其中
，
，
的可能取值为：①
；②
；③
；④
；⑤
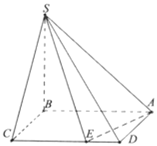
（1）求直线
与平面所成角的正弦值；
（2）若线段CD上能找到点E，满足
的点有两个，分别记为
，
，求二面角
的大小.
【答案】（1）
（2）30°
【解析】
（1）由
底面ABCD，得到
即为直线AS与平面ABCD所成的角，利用正弦函数可得角的正弦值；
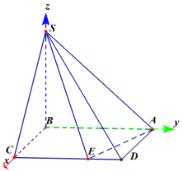
（2）以B为坐标原点，以BC、BA、BS的方向分别为x轴、y轴、z轴正方向建立如图所示的空间直角坐标系，由题意取
时，
是二面角
的平面角，
求得
即为所求答案.
（1）因为底面ABCD，所以即为直线AS与平面ABCD所成的角，
在
中，
.
（2）以B为坐标原点，以BC、BA、BS的方向分别为x轴、y轴、z轴正方向建立如图所示的空间直角坐标系.则各点坐标分别为：
设
，所以，
，
，
.
因为
，
，所以在所给的数据中，
可以取①②③
当，此时，
或
，即满足条件的点E有两个，
根据题意得，其坐标为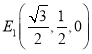
和
，
因为平面ABCD，所以
，
，
所以，是二面角的平面角.
由
，
由题意得二面角为锐角，
所以二面角的大小为30°.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
【题目】某农户计划种植莴笋和西红柿，种植面积不超过
亩，投入资金不超过
万元，假设种植莴笋和西红柿的产量、成本和售价如下表：
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么，该农户一年种植总利润（总利润=总销售收入-总种植成本）的最大值为____万元
