题目内容
19.已知函数f(x)=lnx-$\frac{{{{(x-1)}^2}}}{2}$.(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)证明:当x>1时,f(x)<x-1.
分析 (Ⅰ)求函数f(x)的导数,利用导函数大于0,求解不等式得到函数的单调递增区间;
(Ⅱ)构造函数,利用导数判断函数的单调性,然后证明当x>1时,f(x)<x-1.
解答 (I)解:$f'(x)=\frac{1}{x}-x+1=\frac{{-{x^2}+x+1}}{x}$,x∈(0,+∞).
由f′(x)>0得$\left\{\begin{array}{l}x>0\\-{x^2}+x+1>0\end{array}\right.$解得$0<x<\frac{{1+\sqrt{5}}}{2}$.
故f(x)的单调递增区间是$({0,\frac{{1+\sqrt{5}}}{2}})$.
(II)证明:令F(x)=f(x)-(x-1),x∈(0,+∞).
则有$F'(x)=\frac{{1-{x^2}}}{x}$.当x∈(1,+∞)时,F′(x)<0,
所以F(x)在[1,+∞)上单调递减,
故当x>1时,F(x)<F(1)=0,
即当x>1时,f(x)<x-1.
点评 本题考查函数的导数的应用,函数的单调性与对数的关系,不等式的证明的方法,考查分析问题解决问题的能力.

练习册系列答案
相关题目
10.已知$\vec a=({-3,2}),\vec b=({-1,0})$,向量λ$\vec a+\vec b$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直,则实数λ的值为( )
| A. | $\frac{1}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $-\frac{1}{7}$ |
7.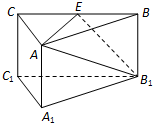 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AC⊥平面ABB1A1 | ||
| C. | A1C1∥平面AB1E | D. | AE,B1C1为异面直线,且AE⊥B1C1 |
14.在△ABC中,a,b,c分别为A,B,C所对的边,且(a+c)(a-c)=b(b+c),则角A=( )
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
4.若不等式$\frac{1}{x}$<2和|x|>$\frac{1}{3}$同时成立,则x的取值范围是( )
| A. | -$\frac{1}{2}$<x<$\frac{1}{3}$ | B. | x>$\frac{1}{2}$或x<-$\frac{1}{3}$ | C. | x>$\frac{1}{2}$或x<$\frac{1}{3}$ | D. | x>$\frac{1}{2}$ |