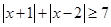题目内容
设函数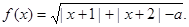
(1)当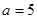 时,求函数
时,求函数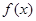 的定义域;
的定义域;
(2)若函数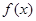 的定义域为R,试求
的定义域为R,试求 的取值范围。
的取值范围。
(1)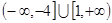 ;(2)
;(2)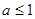 .
.
解析试题分析:
(1)本小题先根据二次根号下非负,可得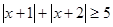 ,然后结合函数的图像可求得函数的定义域;
,然后结合函数的图像可求得函数的定义域;
(2)主要是根据函数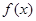 的定义域为R可知当
的定义域为R可知当 时,恒有
时,恒有 成立,于是转化为最值求解,结合函数的图像可得
成立,于是转化为最值求解,结合函数的图像可得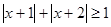 ,进而求得
,进而求得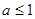 .
.
试题解析:
(1)由题意可知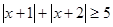
在同一坐标系中作出函数 和
和 的图像
的图像
根据图像可知定义域为
(2)由题意可知
即当 时,恒有
时,恒有 成立
成立
根据(1)可知
所以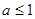
考点:绝对值不等式.

练习册系列答案
相关题目
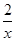 .
.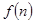 表示,且
表示,且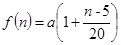 (其中
(其中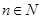 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.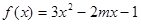 ,
,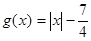 .
.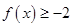 ;
;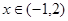 ,
,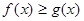 ,求
,求 的取值范围.
的取值范围.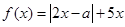 ,其中实数
,其中实数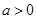 .
.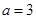 时,求不等式
时,求不等式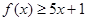 的解集;
的解集;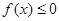 的解集为
的解集为 ,求
,求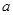 的值.
的值.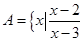 <
<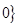 ,
,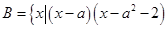 <
< 时,求
时,求 ;
;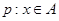 ,命题
,命题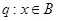 ,若q是p的必要条件,求实数
,若q是p的必要条件,求实数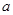 的取值范围.
的取值范围. 的不等式
的不等式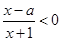 的解集为
的解集为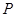 ,不等式
,不等式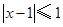 的解集为
的解集为 .
.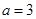 ,求
,求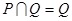 ,求正数
,求正数 的取值.
的取值. ,
,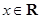 .
.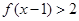 ;
;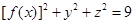 ,试求
,试求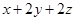 的最小值.
的最小值.