题目内容
已知函数: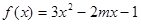 ,
,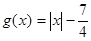 .
.
⑴解不等式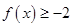 ;
;
⑵若对任意的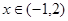 ,
,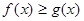 ,求
,求 的取值范围.
的取值范围.
(1) ① 时,不等式的解为R; ②
时,不等式的解为R; ② 或
或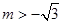 时,
时,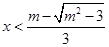 或
或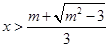 ;(2)
;(2) .
.
解析试题分析:(1)含参数的二次不等式的解法要考虑判别式的值.(2)本题较难就是绝对值的处理,把x的范围按正负分开在讨论,特别是小于零部分的处理要细心,应用基本不等式的知识.
试题解析:⑴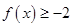 可化为
可化为 ,
, ,
,
①当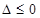 时,即
时,即 时,不等式的解为R;
时,不等式的解为R;
②当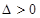 时,即
时,即 或
或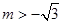 时,
时, ,
, ,
,
不等式的解为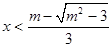 或
或 ;
;
⑵ ,对任意的
,对任意的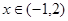 恒成立,
恒成立,
①当 时,
时,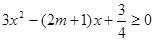 ,即
,即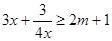 在
在 时恒成立;
时恒成立;
因为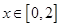 ,当
,当 时等号成立.所以
时等号成立.所以 ,即
,即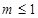 ;
;
②当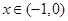 时,
时, ,即
,即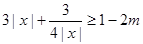 在
在 时恒成立,
时恒成立,
因为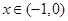 ,当
,当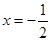 时等号成立.
时等号成立.
所以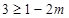 ,即
,即 ;
;
③当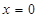 时,
时, .综上所述,实数
.综上所述,实数 的取值范围是
的取值范围是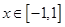 .
.
考点:1.含参的二次不等式的解法.2.含绝对值的不等式恒成立问题.3.分类的思想.

练习册系列答案
相关题目
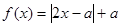 .
.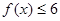 的解集为
的解集为 ,求实数
,求实数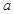 的值;
的值;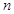 使
使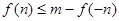 成立,求实数
成立,求实数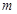 的取值范围.
的取值范围.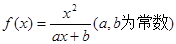 ,且方程
,且方程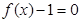 有两个实根为
有两个实根为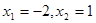 .
. 的解析式 ;
的解析式 ; 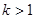 ,解关于x的不等式:
,解关于x的不等式: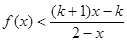 .
. 的不等式
的不等式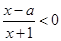 的解集为
的解集为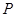 ,不等式
,不等式 的解集为
的解集为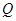 .
.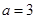 ,求
,求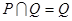 ,求正数
,求正数 的取值.
的取值.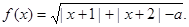
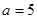 时,求函数
时,求函数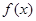 的定义域;
的定义域; 的取值范围。
的取值范围。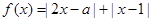 .
.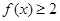 的解集;
的解集;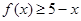 对
对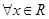 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.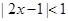 的解集为
的解集为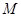 .(I)求集合
.(I)求集合 ,
, ∈
∈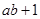 与
与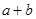 的大小.
的大小.