题目内容
已知函数 ,
,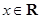 .
.
(Ⅰ)解不等式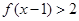 ;
;
(Ⅱ)若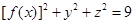 ,试求
,试求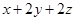 的最小值.
的最小值.
(Ⅰ)原不等式的解集为 或
或 ;(Ⅱ)
;(Ⅱ)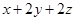 的最小值为
的最小值为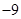 .
.
解析试题分析:(Ⅰ)将原不等式表示出来,借助含绝对值不等式的解法进行求解;(Ⅱ)先将不等式配成柯西不等式的相关形式,然后利用柯西不等式求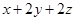 的最小值.
的最小值.
试题解析:(Ⅰ)原不等式化为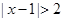 ,
, 或
或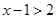 ,即
,即 或
或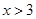 ,
,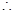 原不等式的解集为
原不等式的解集为 或
或 . 3分
. 3分
(Ⅱ)由已知,得 ,
,
由柯西不等式,得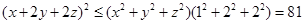 ,
,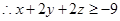 , 5分
, 5分
当且仅当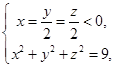 即
即 时等号成立, 6分
时等号成立, 6分
所以,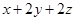 的最小值为
的最小值为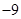 . 7分
. 7分
考点:含绝对值不等式、柯西不等式

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
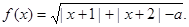
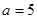 时,求函数
时,求函数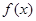 的定义域;
的定义域; 的取值范围。
的取值范围。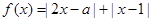 .
.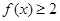 的解集;
的解集;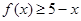 对
对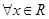 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. ,关于
,关于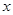 的不等式
的不等式 的解集不是空集,求实数
的解集不是空集,求实数 的取值范围.
的取值范围.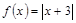 ,
,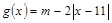 , 若
, 若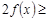
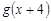 恒成立,实数
恒成立,实数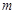 的最大值为
的最大值为 .
.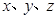 满足
满足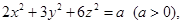 且
且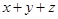 的最大值是
的最大值是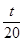 ,求
,求 的值.
的值.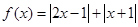
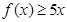 ;
;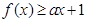 的解集为
的解集为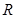 ,求实数
,求实数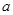 的取值范围
的取值范围 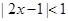 的解集为
的解集为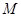 .(I)求集合
.(I)求集合 ,
, ∈
∈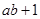 与
与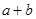 的大小.
的大小.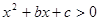 的解集为
的解集为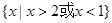
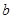 和
和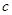 的值; (2)求不等式
的值; (2)求不等式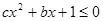 的解集.
的解集.