题目内容
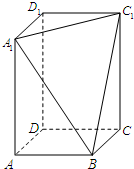 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.(1)求棱A1A的长;
(2)求此几何体的表面积,并画出此几何体的主视图和俯视图(写出各顶点字母).
分析:(1)设长方体的高AA1=h,根据长方体体积公式和锥体体积公式列方程,解之即可得到AA1=3.
(2)根据题意,可得该几何体的表面由三个长方形和四个三角形组成,分别求出各长方形和三角形的面积,相加即得此几何体的表面积,再根据三视图的定义可作出它的主视图和俯视图.
(2)根据题意,可得该几何体的表面由三个长方形和四个三角形组成,分别求出各长方形和三角形的面积,相加即得此几何体的表面积,再根据三视图的定义可作出它的主视图和俯视图.
解答:解:(1)设长方体的高AA1=h,则该几何体体积为
VABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1B1C1=10--------------------2'
即2×2•h-
×
×2×2×h=
h=10,解得:h=3,即AA1=3-----------------------6’
(2)根据题意,可得该几何体的表面由三个长方形和四个三角形组成,
SAA1D1D=SC1D1DC=2×3=6,SABCD=2×2=4,
S△A1AB=S△BC1C=
×2×3=3,S△A1D1C1=
×2×2=2,
在△A1BC1中,A1B=
=
=BC1,A1C1=
=2
∴cos∠A1BC1=
=
,
可得sin∠A1BC1=
=
所以S△A1BC1=
×
×
×
=
由此可得该几何体的表面积为:
S表=SAA1D1D+SC1D1DC+SABCD+S△A1AB+S△BC1C+S△A1D1C1+S△A1BC1=24+
---------------------------10'
几何体的主视图和俯视图如右图所示(主视图和俯视图分别为2分).---------------------------14'
VABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1B1C1=10--------------------2'
即2×2•h-
| 1 |
| 3 |
| 1 |
| 2 |
| 10 |
| 3 |

(2)根据题意,可得该几何体的表面由三个长方形和四个三角形组成,
SAA1D1D=SC1D1DC=2×3=6,SABCD=2×2=4,
S△A1AB=S△BC1C=
| 1 |
| 2 |
| 1 |
| 2 |
在△A1BC1中,A1B=
| 22+32 |
| 13 |
| 22+22 |
| 2 |
∴cos∠A1BC1=
| 13+13-8 | ||||
2×
|
| 9 |
| 13 |
可得sin∠A1BC1=
1-(
|
2
| ||
| 13 |
所以S△A1BC1=
| 1 |
| 2 |
| 13 |
| 13 |
2
| ||
| 13 |
| 22 |
由此可得该几何体的表面积为:
S表=SAA1D1D+SC1D1DC+SABCD+S△A1AB+S△BC1C+S△A1D1C1+S△A1BC1=24+
| 22 |
几何体的主视图和俯视图如右图所示(主视图和俯视图分别为2分).---------------------------14'
点评:本题将长方体切去一个角,在已知体积的情况下求它的高,并求几何体的表面积,着重考查了棱柱棱锥的体积公式,用正余弦定理求三角形面积等知识,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.