题目内容
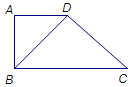
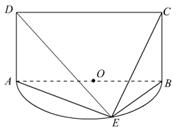
在直角梯形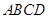 中,
中,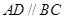 ,
,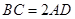
 ,
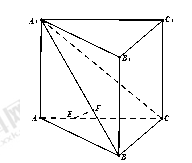
,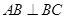 ,如图,把
,如图,把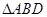 沿
沿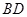 翻折,使得平面
翻折,使得平面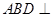 平面
平面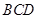 .
.
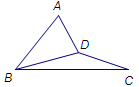
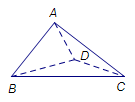
(1)求证: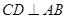 ;
;
(2)若点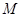 为线段
为线段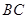 中点,求点
中点,求点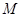 到平面
到平面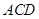 的距离;
的距离;
(3)在线段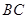 上是否存在点
上是否存在点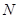 ,使得
,使得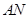 与平面
与平面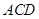 所成角为
所成角为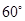 ?若存在,求出
?若存在,求出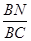 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)证明过程详见解析;(2)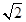 (3)存在
(3)存在 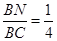
解析试题分析:
(1)据题意,要证明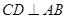 ,由线面垂直的性质例一得到只需要证明DC
,由线面垂直的性质例一得到只需要证明DC 面ABD,又有面ABD与面BCD垂直,故根据面面垂直的性质,只需要证明DC垂直于面ABD与面BCD的交线BD,DC与BC垂直的证明可以放在直角梯形
面ABD,又有面ABD与面BCD垂直,故根据面面垂直的性质,只需要证明DC垂直于面ABD与面BCD的交线BD,DC与BC垂直的证明可以放在直角梯形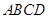 中利用勾股定理与余弦定理证明,三角形BCD为直角三角形.
中利用勾股定理与余弦定理证明,三角形BCD为直角三角形.
(2)由(1)得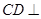 平面
平面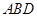 ,所以
,所以 .以点
.以点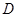 为原点,
为原点,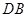 所在的直线为
所在的直线为 轴,
轴,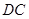 所在直线为
所在直线为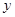 轴,利用三维空间直角坐标系即可求的点面距离,即首先求出线段MC与面ADC的法向量的夹角,再利用三角函数值即可求的点面距离.此外,该题还可以利用等体积法来求的点面距离,即三棱锥M-ADC的体积,分别以M点为顶点和以A点为定点来求解三棱锥的体积,解出高即为点面距离.
轴,利用三维空间直角坐标系即可求的点面距离,即首先求出线段MC与面ADC的法向量的夹角,再利用三角函数值即可求的点面距离.此外,该题还可以利用等体积法来求的点面距离,即三棱锥M-ADC的体积,分别以M点为顶点和以A点为定点来求解三棱锥的体积,解出高即为点面距离.
(3)该问利用坐标法最为简洁,在第二问建立的坐标系的基础上,设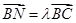 ,
,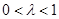 ,利用
,利用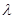 来表示N点的坐标,求出面ACD的法向量,法向量与AN所成的夹角即为
来表示N点的坐标,求出面ACD的法向量,法向量与AN所成的夹角即为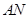 与平面
与平面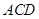 所成角为
所成角为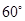 的余角,利用该条件即可求出
的余角,利用该条件即可求出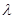 的值,进而得到N点的位置.
的值,进而得到N点的位置.
试题解析:
(1)证明:因为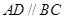 ,
,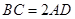
 ,
,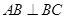 ,所以
,所以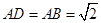 ,
,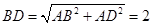 ,
,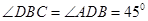 1分
1分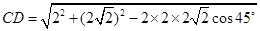
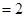 , 2分
, 2分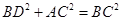 ,所以
,所以 3分.
3分.
因为平面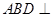 平面
平面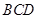 ,平面
,平面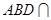 平面
平面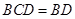 ,
,
所以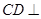 平面
平面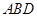 4分.
4分.
又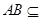 平面
平面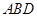 ,所以
,所以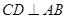 5分.
5分.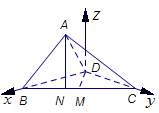
(2)解法1:因为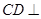 平面
平面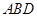 ,所以
,所以 .以点
.以点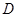 为原点,
为原点,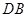 所在的直线为
所在的直线为 轴,
轴,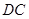 所在直线为
所在直线为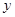 轴,过点
轴,过点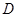 作垂直平面
作垂直平面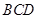 的直线为
的直线为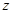 轴,建立空间直角坐标系
轴,建立空间直角坐标系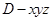 ,如图.由已知,得
,如图.由已知,得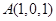 ,
,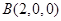 ,
,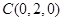 ,
,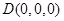 ,
,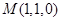 .所以
.所以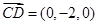 ,
,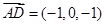 ,
,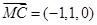 . 7分.设平面
. 7分.设平面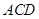 的法向量为
的法向量为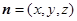 ,则
,则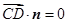 ,
,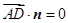 ,所以
,所以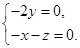 令
令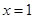 ,得平面
,得平面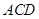 的一个法向量为
的一个法向量为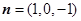 9分
9分
所以点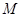

 优等生题库系列答案
优等生题库系列答案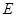 是以
是以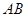 为直径的半圆
为直径的半圆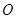 上异于
上异于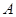 、
、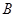 的点,矩形
的点,矩形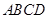 所在的平面垂直于半圆
所在的平面垂直于半圆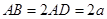 .
.
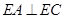 ;
;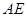 和
和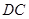 所成的角为
所成的角为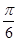 ,求平面
,求平面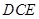 与平面
与平面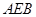 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
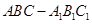 (侧棱和底面垂直的棱柱)中,
(侧棱和底面垂直的棱柱)中,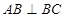 ,
,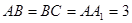 ,
,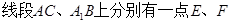 ,且满足
,且满足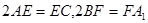 .
.
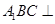 侧面
侧面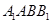 ;
;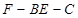 的平面角的余弦值。
的平面角的余弦值。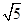 ,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=
,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=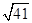 .
.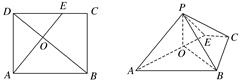
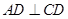 ,
,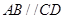 ,
,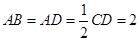 ,点M在线段EC上(除端点外)
,点M在线段EC上(除端点外)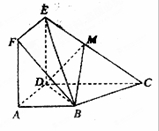
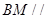 平面
平面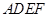 ;
;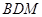 与平面ABF所成二面角为锐角,且该二面角的余弦值为
与平面ABF所成二面角为锐角,且该二面角的余弦值为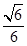 时,求三棱锥
时,求三棱锥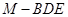 的体积
的体积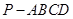 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中 ,
,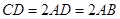 ,平面
,平面 底面
底面 是
是 的中点.
的中点.
 //平面
//平面 ;
; 与平面BDE所成角的余弦值;
与平面BDE所成角的余弦值;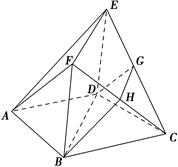
 是边长为3的正方形,
是边长为3的正方形, ,
,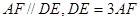 ,
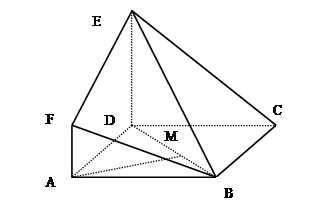
,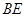 与平面
与平面 .
.
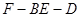 的的余弦值;
的的余弦值;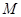 是线段
是线段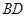 上一动点,试确定
上一动点,试确定 ,并证明你的结论.
,并证明你的结论.