题目内容
【题目】圆周上分布着2014个点,将其任意染成红、黄两色.若从某一点开始,依任一方向绕圆周运动到任一位置,所经过的点(含自身)红点个数恒大于黄点个数,则称该点为“优点”.为确保圆周上至少有一个优点,求圆周上黄点个数的最大值.
【答案】671
【解析】
优点一定为红点.
首先考虑简单情形.
当圆周上分别有1、2、3、4、5,6、7个点时,若圆周上至少有一个优点,则圆周上黄点个数最大值分别为0、0、0、1、1、1、2.
由此,得到一般性结论：圆周上有
个点,将其任意染成红、黄两色.当且仅当黄点个数不大于
时,才能保证圆周上至少有一个优点存在.
接下来用数学归纳法给出证明.当
时,圆周上有四个点(一个黄点三个红点),在三个相连的红点中取居中的那个,易知,其为优点.故时命题成立.
假设当
时,命题成立,即圆周上有
个点,分别染成红、黄两色,为确保圆周上至少有一个优点,则黄点个数不超过
.
当
时,在
个黄点中任取一个,记为
.在两旁分别取与最近的红点,分别记为
.将此三点从圆周上拿走,则在圆周上只剩下个点,且满足时命题成立的条件.
由归纳假设,知圆周上至少存在一个优点,记为
.再把
三点放回原位置.
下面证明：点仍为优点.
因为为红点,所以,点必在弧
外.因此,从点出发到弧
()上任一位置,红点个数与黄点个数之差至少大于1,到点时至少大于0.故仍为优点.
从而,当时,命题成立.
另一方面,在个点中,若黄点个数为
,将圆周分成段,将
个红色点放入每一段弧中,每段弧中至多两个点,则每个红点均不可能为优点.
因此,圆周上黄点个数的最大值为.
又
,则圆周上黄点个数的最大值为671.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某市的教育主管部门对所管辖的学校进行年终督导评估，为了解某学校师生对学校教学管理的满意度，分别从教师和不同年级的同学中随机抽取若干师生，进行评分(满分100分)，绘制如下频率分布直方图(分组区间为
， 
， 
， 
， 
， 
)，并将分数从低到高分为四个等级：
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.
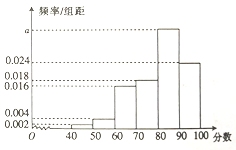
(1)求表中
的值及不满意的人数；
(2)在等级为不满意的师生中，老师占
，现从该等级师生中按分层抽样抽取12人了解不满意的原因，并从中抽取3人担任整改督导员，记
为老师整改督导员的人数，求
的分布列及数学期望.
【题目】某大型电器企业，为了解组装车间职工的生活情况，从中随机抽取了
名职工进行测试，得到频数分布表如下：
日组装个数 |
|
|
|
|
|
|
人数 | 6 | 12 | 34 | 30 | 10 | 8 |
（1）现从参与测试的日组装个数少于
的职工中任意选取
人，求至少有
人日组装个数少于
的概率；
（2）由频数分布表可以认为，此次测试得到的日组装个数
服从正态分布
，
近似为这人得分的平均值（同一组数据用该组区间的中点值作为代表）.
（
名职工，求日组装个数超过
的职工人数；
（ii）为鼓励职工提高技能，企业决定对日组装个数超过
的职工日工资增加
元，若在组装车间所有职工中任意选取人，求这三人增加的日工资总额的期望.
附：若随机变量
服从正态分布
，则
，
，
.
【题目】某市环保部门对该市市民进行了一次动物保护知识的网络问卷调查，每位市民仅有一次参加机会，通过随机抽样，得到参'与问卷调查的100人的得分（满分：100分）数据，统计结果如表所示：
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 15 | 5 | 10 |
若规定问卷得分不低于70分的市民称为“动物保护关注者”，则山图中表格可得
列联表如下：
非“动物保护关注者” | 是“动物保护关注者” | 合计 | |
男 | 10 | 45 | 55 |
女 | 15 | 30 | 45 |
合计 | 25 | 75 | 100 |
（1）请判断能否在犯错误的概率不超过0．05的前提下认为“动物保护关注者”与性别有关？
（2）若问卷得分不低于80分的人称为“动物保护达人”．现在从本次调查的“动物保护达人”中利用分层抽样的方法随机抽取6名市民参与环保知识问答，再从这6名市民中抽取2人参与座谈会，求抽取的2名市民中，既有男“动物保护达人”又有女“动物保护达人”的概率．
附表及公式：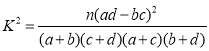
，其中
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
