题目内容
1.直线a,b的方向向量分别为$\overrightarrow{e}$=(1,-2,-2),$\overrightarrow{n}$=(-2,-3,2),则a与b的位置关系是( )| A. | 平行 | B. | 重合 | C. | 垂直 | D. | 夹角等于$\frac{π}{3}$ |
分析 由$\overrightarrow{e}•\overrightarrow{n}$=0,可得$\overrightarrow{e}⊥\overrightarrow{n}$,即可判断出位置关系.
解答 解:∵$\overrightarrow{e}•\overrightarrow{n}$=-2+6-4=0,
∴$\overrightarrow{e}⊥\overrightarrow{n}$,
∴a⊥b.
故选:C.
点评 本题考查了向量垂直与数量积的关系、直线的方向向量,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
12.球面上有A、B、C、D四个点,若AB、AC、AD两两垂直,且AB=AC=AD=4,则该球的表面积为( )
| A. | $\frac{80π}{3}$ | B. | 32π | C. | 42π | D. | 48π |
9.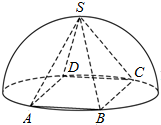 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为.( )
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为.( )
 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为.( )
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为.( )| A. | $\frac{4\sqrt{2}}{3}$π | B. | $\frac{8\sqrt{2}}{3}$π | C. | $\frac{32\sqrt{2}}{3}$π | D. | $\frac{64\sqrt{2}}{3}$π |
16.下列函数中,既是奇函数又是减函数的是( )
| A. | $y=\frac{1}{x}$ | B. | y=-tanx | C. | $y=\frac{{1-{2^x}}}{{1+{2^x}}}$ | D. | y=-x3(-1<x≤1) |
13.“依法纳税是每个公民应尽的义务”,国家征收个人工资、薪金所得税是分段计算的:总收入不超过800元的,免征个人工资、薪金所得税;超过800元部分需征税,设纳税所得额(所得额指月工资、薪金中应纳税的部分)为x,x=全月总收入-800(元),税率见下表:
(1)若应纳税额为f(x),试用分段函数表示1~3级纳税额f(x)的计算公式;
(2)某人2004年10月份工资总收入为4000元,试计算这个人10月份应纳个人所得税多少元?
| 级数 | 全月应纳税所得额x | 税率 |
| 1 | 不超过500元部分 | 5% |
| 2 | 超过500元至2000元部分 | 10% |
| 3 | 超过2000元至5000元部分 | 15% |
| … | … | … |
| 9 | 超过100000元部分 | 45% |
(2)某人2004年10月份工资总收入为4000元,试计算这个人10月份应纳个人所得税多少元?