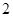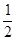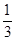题目内容
若数列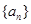 的前n项和为
的前n项和为 ,则下列命题:
,则下列命题:
(1)若数列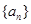 是递增数列,则数列
是递增数列,则数列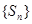 也是递增数列;
也是递增数列;
(2)数列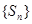 是递增数列的充要条件是数列
是递增数列的充要条件是数列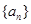 的各项均为正数;
的各项均为正数;
(3)若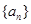 是等差数列(公差
是等差数列(公差 ),则
),则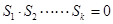 的充要条件是
的充要条件是
(4)若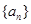 是等比数列,则
是等比数列,则 的充要条件是
的充要条件是
其中,正确命题的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
B
解析试题分析:数列{an}的前n项和为Sn,故 Sn =a1+a2+a3+…+an.若数列{an}是递增数列,则数列{Sn}不一定是递增数列,如当an<0 时,数列{Sn}是递减数列,故(1)不正确;由数列{Sn}是递增数列,不能推出数列{an}的各项均为正数,如数列:0,1,2,3,…,满足{Sn}是递增数列,但不满足数列{an}的各项均为正数,故(2)不正确;若{an}是等差数列(公差d≠0),则由S1•S2…Sk=0,不能推出a1•a2…ak=0,例如数列:-3,-1,1,3,满足S4=0,但 a1•a2•a3•a4≠0,故(3)不正确.若{an}是等比数列,则由S1•S2…Sk=0(k≥2,k∈N)可得数列的{an}公比为-1,故有an+an+1=0.由an+an+1=0可得数列的{an}公比为-1,可得S1•S2…Sk=0(k≥2,k∈N),故(4)正确.故选B.
考点:1.等比数列的性质;2. 等差数列的性质;3.充分必要条件.

练习册系列答案
相关题目
设数列{an},则有( )
A.若 =4n,n∈N*,则{an}为等比数列 =4n,n∈N*,则{an}为等比数列 |
B.若an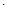 an+2= an+2=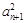 ,n∈N*,则{an}为等比数列 ,n∈N*,则{an}为等比数列 |
C.若am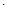 an=2m+n,m,n∈N*,则{an}为等比数列 an=2m+n,m,n∈N*,则{an}为等比数列 |
D.若an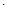 an+3=an+1 an+3=an+1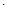 an+2,n∈N*,则{an}为等比数列 an+2,n∈N*,则{an}为等比数列 |
在各项都为正数的等比数列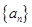 中,
中,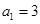 ,前三项的和为
,前三项的和为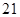 ,则
,则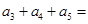 ( )
( )
A.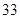 | B.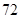 | C. | D.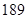 |
数列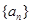 的首项为1,数列
的首项为1,数列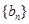 为等比数列且
为等比数列且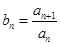 ,若
,若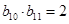 ,则
,则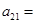 ( )
( )
| A.20 | B.512 | C.1013 | D.1024 |
已知等比数列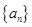 的公比
的公比 ,且
,且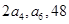 成等差数列,则
成等差数列,则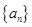 的前8项和为( )
的前8项和为( )
| A.127 | B.255 | C.511 | D.1023 |
数列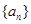 的首项为1,数列
的首项为1,数列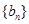 为等比数列且
为等比数列且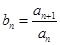 ,若
,若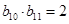 ,则
,则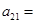 ( )
( )
| A.20 | B.512 | C.1013 | D.1024 |
已知等差数列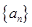 的前项和为
的前项和为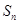 ,且
,且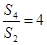 ,则
,则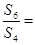 ( )
( )
A.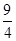 | B.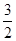 | C.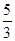 | D.4 |
已知各项均为正数的等比数列{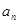 },
},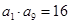 ,则
,则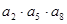 的值为( )
的值为( )
| A.16 | B.32 | C.48 | D.64 |
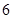 项和是前
项和是前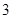 项和的
项和的 倍,则此数列的公比为( )
倍,则此数列的公比为( )