题目内容
(本小题满分12分)已知函数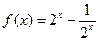 .
.
(1)若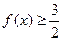 ,求x的取值范围;
,求x的取值范围;
(2)若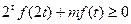 对于
对于 ∈[1,2]恒成立,求实数m的取值范围.
∈[1,2]恒成立,求实数m的取值范围.
解:(1)当x<0时,f(x)=0;
当x≥0时,f(x)=2x-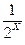 .
.
由条件可知2x-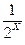 》2,即22x-1.5·2x-1》0,
》2,即22x-1.5·2x-1》0,
解得2x》2
∵2x>0,∴x》1.
(2)当t∈[1,2]时,2t +m
+m ≥0,
≥0,
即m(22t-1)≥-(24t-1).
∵22t-1>0,∴m≥-(22t+1).
∵t∈[1,2],∴-(1+22t)∈[-17,-5],
故m的取值范围是[-5,+∞).
解析

练习册系列答案
相关题目
函数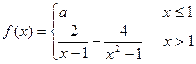 在x=1处连续,则
在x=1处连续,则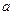 =
=
A. | B.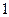 | C. | D.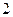 |
 .
. 在
在 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围;
的取值范围; 时,
时, 上的最小值为
上的最小值为 ,求
,求 设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
设g(x)=f(x)-2x2,求证函数g(x)只有一个零点. -bx+4,当x=2时,函数f(x)有极值-.
-bx+4,当x=2时,函数f(x)有极值-. x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0. )求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.
)求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.
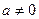 时,求:函数
时,求:函数 的单调区间;
的单调区间; 时,求证:当
时,求证:当 时,不等式
时,不等式
 x)能否由y=log3x的图象平移变换得到;
x)能否由y=log3x的图象平移变换得到;
 元)与隔热层厚度x(单位:cm)
元)与隔热层厚度x(单位:cm) ②若不建隔热层,每年能源消耗费用为8万
②若不建隔热层,每年能源消耗费用为8万