题目内容
 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=
| ||
| 2 |
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD⊥平面ADE;
(3)在CD上是否存在一点M,使得MO∥平面ADE?证明你的结论.
分析:(1)求三棱锥C-ABE的体积,转化为求E-ABC的体积,求出底面面积,即可解答本题.
(2)要证明:平面ACD⊥平面ADE,只需证明DE⊥平面ADC,先证DE垂直AC和DC即可.
(3)点M为DC的中点,使得MO∥平面ADE,取BE的中点N,连MO、MN、NO,证明平面MNO∥平面ADE,即可.
(2)要证明:平面ACD⊥平面ADE,只需证明DE⊥平面ADC,先证DE垂直AC和DC即可.
(3)点M为DC的中点,使得MO∥平面ADE,取BE的中点N,连MO、MN、NO,证明平面MNO∥平面ADE,即可.
解答: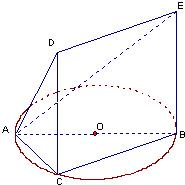 解:(1)∵四边形DCBE为平行四边形∴CD∥BE
解:(1)∵四边形DCBE为平行四边形∴CD∥BE
∵DC⊥平面ABC∴BE⊥平面ABC
∴∠EAB为AE与平面ABC所成的角,
即∠EAB=θ
在Rt△ABE中,由tanθ=
=
,
AB=2得BE=
∵AB是圆O的直径∴BC⊥AC
∴AC=
=
∴S△ABC=
AC•BC=
∴VC-ABE=VE-ABC=
S△ABC• BE=
×
×
=
(2)证明:∵DC⊥平面ABC,BC?平面ABC∴DC⊥BC.(6分)
∵BC⊥AC且DC∩AC=C∴BC⊥平面ADC、
∵DE∥BC∴DE⊥平面ADC
又∵DE?平面ADE∴平面ACD⊥平面ADE;
(3)在CD上存在点M,使得MO∥平面ADE,该点M为DC的中点.
证明如下:如图,取BE的中点N,连MO、MN、NO,
∵M、N、O分别为CD、BE、AB的中点,
∴.MN∥DE
∵DE?平面ADE,MN不在平面ADE,
∴MN∥平面ADE
同理可得NO∥平面ADE.
∵MN∩NO=N,∴平面MNO∥平面ADE.
∵MO?平面MNO,∴MO∥平面ADE.
 解:(1)∵四边形DCBE为平行四边形∴CD∥BE
解:(1)∵四边形DCBE为平行四边形∴CD∥BE∵DC⊥平面ABC∴BE⊥平面ABC
∴∠EAB为AE与平面ABC所成的角,
即∠EAB=θ
在Rt△ABE中,由tanθ=
| BE |
| AB |
| ||
| 2 |
AB=2得BE=
| 3 |
∵AB是圆O的直径∴BC⊥AC
∴AC=
| AB2-BC2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
∴VC-ABE=VE-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
(2)证明:∵DC⊥平面ABC,BC?平面ABC∴DC⊥BC.(6分)
∵BC⊥AC且DC∩AC=C∴BC⊥平面ADC、
∵DE∥BC∴DE⊥平面ADC
又∵DE?平面ADE∴平面ACD⊥平面ADE;
(3)在CD上存在点M,使得MO∥平面ADE,该点M为DC的中点.
证明如下:如图,取BE的中点N,连MO、MN、NO,
∵M、N、O分别为CD、BE、AB的中点,
∴.MN∥DE
∵DE?平面ADE,MN不在平面ADE,
∴MN∥平面ADE
同理可得NO∥平面ADE.
∵MN∩NO=N,∴平面MNO∥平面ADE.
∵MO?平面MNO,∴MO∥平面ADE.
点评:本题考查棱锥的体积,只需与平面平行与垂直的证明,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
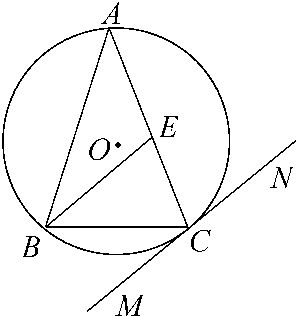 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.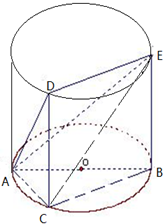 如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=
如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=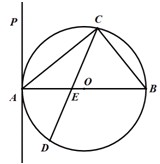 (2013•沈阳二模)选修4-1:几何证明选讲
(2013•沈阳二模)选修4-1:几何证明选讲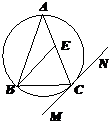 如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )
如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )